Một chất điểm chuyển động tròn đều với tốc độ 0,75m/s trên đường tròn bán kính 0,25m. Hình chiếu M’ của điểm M lên đường kính của đường tròn dđđh. Biết tại thời điểm ban đầu, M’ đi qua vị trí x=A/2 theo chiều âm. Tại thời điểm t=8s hình chiếu M’ qua li độ:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án C
y = O M sin ( ω t + φ ) = 10 sin 2 π t + π 6 = 10 cos 2 π t − π 3 ( c m )

Đáp án D
+ Phương trình dao động của hình chiếu M lên Oy: y = 10 cos 2 πt − π 3

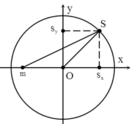

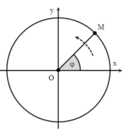
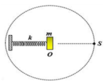
Chọn gốc thời gian là khi trạng thái dao động của hệ như hình vẽ → phương trình dao động của vật và hình chiếu của S theo phương ngang Ox là:

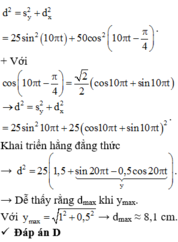

Đáp án D
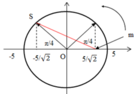
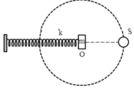
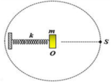
- S chuyển động tròn đều trên đường tròn tâm O bán kính 5cm với tốc độ góc 10π (rad/s)
- Vật m dao động điều hoà với với:
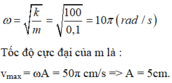
- Tại thời điểm nào đó, điểm sáng S đang đi qua vị trí như trên hình vẽ, còn vật nhỏ m đang có tốc độ cực đại (m có tốc độ cực đại khi qua vị trí cân bằng) => S và m luôn lệch pha nhau góc π/2.
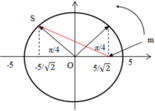
S và m cách nhau lớn nhất khi m và S đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác ta có:
Áp dụng định lí Py – ta – go, ta có khoảng cách lớn nhất giữa S và m (đường màu đỏ) là:
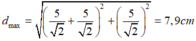

- S chuyển động tròn đều trên đường tròn tâm O bán kính 5cm với tốc độ góc 10π (rad/s)
- Vật m dao động điều hoà với với:
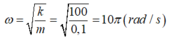
Tốc độ cực đại của m là : vmax = ωA = 50π cm/s => A = 5cm.
- Tại thời điểm nào đó, điểm sáng S đang đi qua vị trí như trên hình vẽ, còn vật nhỏ m đang có tốc độ cực đại (m có tốc độ cực đại khi qua vị trí cân bằng) => S và m luôn lệch pha nhau góc π/2.
S và m cách nhau lớn nhất khi m và S đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác ta có :
Áp dụng định lí Py – ta – go, ta có khoảng cách lớn nhất giữa S và m (đường màu đỏ) là :
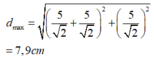
Đáp án D
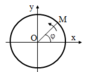
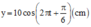
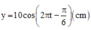
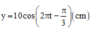
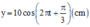
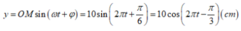

v=ω.r => 0,75=ω.0,25 =>ω=3(rad/s)
A=r=0,25m=25cm
tại thời điểm ban đầu M’ đi qua vị trí x=A/2 theo chiều âm =>φ=\(\dfrac{\pi}{3}\)
pt li độ:x=25cos(3t+\(\dfrac{\pi}{3}\))
tại t=8s => x\(\approx\)24,9(cm)