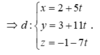Trên mặt phẳng cho 3 điểm X,Y,Z thẳng hàng và 3 điểm M,N,P thỏa mãn XN//YP, YM//ZN, XM//ZP. chứng minh M,N,P thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2016
Mình vẽ được 2 hình dưới nhưng hình bên trái phù hợp với đpcm .Phải sửa đề thành : Trên nửa mặt phẳng bờ BM chứa C lấy điểm N sao cho góc BMN,BDE bù nhau.
góc BDE = góc BAC (2 góc đồng vị của AC // DE) mà góc BMC,góc BAC bù nhau ; góc BMN,góc BDE bù nhau (gt)
=> góc BMC = góc BMN mà 2 tia MN,MC nằm trên cùng nửa mặt phẳng bờ BM (do gt) => MN,MC trùng nhau hay M,N,C thẳng hàng.
NT
1
30 tháng 12 2020
Gọi (MN): y=ax+b
Thay x=1 và y=1 vào hàm số y=ax+b, ta được:
a+b=1
hay a=1-b
Thay x=2 và y=-2 vào hàm số y=ax+b, ta được:
\(2a+b=-2\)
\(\Leftrightarrow2\left(1-b\right)+b=-2\)
\(\Leftrightarrow2-2b+b+2=0\)
\(\Leftrightarrow4-b=0\)
hay b=4
Thay b=4 vào biểu thức a=1-b, ta được:
a=1-4=-3
Vậy: (MN): y=-3x+4
Thay x=-1 và y=7 vào hàm số y=-3x+4, ta được:
\(-3\cdot\left(-1\right)+4=7\)
\(\Leftrightarrow3+4=7\)(đúng)
Vậy: M,N,P thẳng hàng(đpcm)