Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
YCBT: y ' = cos x - sin x + m ≥ 0 với mọi x ∈ ℝ ⇔ m ≥ sin x - cos x = f x với x ∈ ℝ .
Mà ta có: f x = sin x - cos x = 2 x - π 4 ⇒ - 2 ≤ f x ≤ 2 ⇒ m ≥ 2
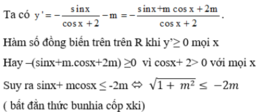
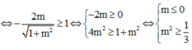
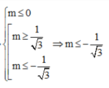
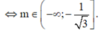
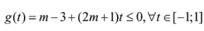
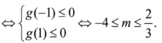
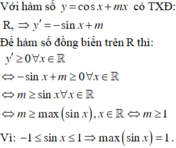




\(y=mx-\left(2m-3\right)cosx\)
\(y'=m+\left(2m-3\right)sinx\)
Để hàm số đồng biến trên \(ℝ\)thì \(y'\ge0\)với mọi \(x\inℝ\).
\(m+\left(2m-3\right)sinx\ge0\)với mọi \(x\inℝ\)(1)
Vì \(-1\le sinx\le1\)nên ta có:
Với \(2m-3\ge0\Leftrightarrow m\ge\frac{3}{2}\)thì
(1) tương đương với \(m-\left(2m-3\right)\ge0\)
\(\Leftrightarrow m\le3\)
suy ra \(\frac{3}{2}\le m\le3\).
Với \(2m-3< 0\Leftrightarrow m< \frac{3}{2}\):
(1) tương đương với: \(m+\left(2m-3\right)\ge0\)
\(\Leftrightarrow m\ge1\)
suy ra \(1\le m< \frac{3}{2}\).
Vậy ...