\(\text{Tính các góc của tứ giác ABCD biết 2 Â =3B=4C=6D}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tứ giác ABCD có : góc A + góc B + góc C + góc D = 3600
(góc A + góc B) + (góc A - góc B) = 1050 + 150
2.góc A = 1200 => góc A = 600 => góc B = 1050 - 600 = 450
góc C + góc D = 3600 - (góc A + góc B)
2.góc D + góc D = 3600 - 1050
3.góc D = 2550 => góc D = 850 => góc C = 850.2 = 1700
A + B = 1050
A - B = 150
A = (1050 + 150) : 2 = 600
B = (1050 - 150) : 2 = 450
Tứ giác ABCD có:
A + B + C + D = 3600
600 + 450 + C + D = 3600
C + D = 3600 - 1050
C + D = 2550
\(C=2D\Rightarrow\frac{C}{2}=\frac{D}{1}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{C}{2}=\frac{D}{1}=\frac{C+D}{2+1}=\frac{255^0}{3}=85^0\)
\(\frac{C}{2}=85^0\Rightarrow C=85^0\times2=170^0\)
\(\frac{D}{1}=85^0\Rightarrow D=85^0\)
Vậy \(A=60^0;B=45^0;C=170^0;D=85^0\)


TH1: ABCD không phải là hình thoi hoặc hình vuông
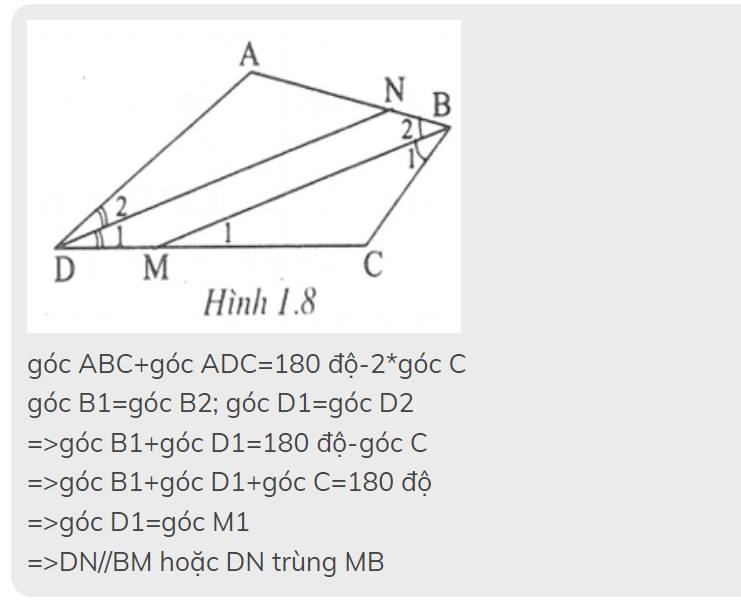
Gọi BM,DN lần lượt là phân giác của \(\widehat{ABC};\widehat{ADC}\)
Xét tứ giác ABCD có
\(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(2\cdot\left(\widehat{NBM}+\widehat{NDM}\right)=360^0-\widehat{A}-\widehat{C}=360^0-2\cdot\widehat{C}\)
=>\(\widehat{NBM}+\widehat{NDM}=180^0-\widehat{C}\)(1)
Xét ΔCMB có
\(\widehat{C}+\widehat{CMB}+\widehat{CBM}=180^0\)
=>\(\widehat{CMB}+\widehat{NBM}=180^0-\widehat{C}\)(2)
Từ (1) và (2) suy ra \(\widehat{NDM}=\widehat{CMB}\)
mà hai góc này ở vị trí đồng vị
nên BM//DN (ĐPCM)
TH2: ABCD là hình thoi hoặc hình vuông
ABCD là hình thoi
=>BD là tia phân giác của \(\widehat{ABC}\) và DB là tia phân giác của \(\widehat{ADC}\)
=>Các đường phân giác của góc B và góc D trùng nhau

Vì A = 2B mà B = 4C nên A = 8C
Vì B = 4C mà D = B + 20 nên D = 4C + 20
Theo bài ra ta có : A + B + C + D = 360o
<=> 8C + 4C + C + 4C + 20 = 360o
<=> 17C = 340o
=> C = 20o
=> B = 80o
=> D = 100o
=> A = 160o
\(2A=3B=4C=6D\Rightarrow\frac{A}{2}=\frac{B}{3}=\frac{C}{3}=\frac{D}{6}\)
Áp dụng tc của dãy tỉ số bằng nhau:
\(\frac{A}{2}=\frac{B}{3}=\frac{C}{4}=\frac{D}{6}=\frac{A+B+C+D}{2+3+4+6}=\frac{360}{15}=24\)
\(\frac{A}{2}=24\Rightarrow A=48\)
\(\frac{B}{3}=24\Rightarrow B=72\)
\(\frac{C}{4}=24\Rightarrow C=96\)
\(\frac{D}{6}=24\Rightarrow D=144\)
Vậy góc A = 48 độ
góc B = 72 độ
góc C = 96 độ
góc D = 144 độ