Trong mp Oxy, cho A(-2;5),B(3;-1), C(7;1).Tìm M thuộc Ox thỏa /vecto MA+vtMB+vtMC/ đật giá trị nhỏ nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NA
2
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 1
Do I thuộc Oy nên tọa độ có dạng \(I\left(0;y\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=\left(1;3-y\right)\\\overrightarrow{BI}=\left(2;y+3\right)\end{matrix}\right.\)
\(\Rightarrow IA+IB=\sqrt{1+\left(3-y\right)^2}+\sqrt{2^2+\left(y+3\right)^2}\ge\sqrt{\left(1+2\right)^2+\left(3-y+y+3\right)^2}=3\sqrt{5}\)
Dấu "=" xảy ra khi \(\dfrac{2}{1}=\dfrac{y+3}{3-y}\Rightarrow y=1\Rightarrow I\left(0;1\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 1
Cách khác:
Do A và B nằm khác phía so với Oy
\(\Rightarrow IA+IB\) đạt giá trị nhỏ nhất khi A, I, B thẳng hàng
Hay I là giao điểm của đường thẳng AB và trục Oy
\(\overrightarrow{BA}=\left(3;6\right)=3\left(1;2\right)\Rightarrow\) đường thẳng AB nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x-1\right)-1\left(y-3\right)=0\Leftrightarrow2x-y+1=0\)
I là giao điểm AB và Oy nên tọa độ là nghiệm của hệ:
\(\left\{{}\begin{matrix}2x-y+1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
\(\Rightarrow I\left(0;1\right)\)
Q
1
Q
1
24 tháng 4 2023
\(AB=\sqrt{\left(1+1\right)^2+\left(2-2\right)^2}=2\)
\(AC=\sqrt{\left(2+1\right)^2+\left(-3-2\right)^2}=\sqrt{34}\)
\(BC=\sqrt{\left(2-1\right)^2+\left(-3-2\right)^2}=\sqrt{26}\)
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{3}{\sqrt{34}}\)
=>\(sinBAC=\dfrac{5\sqrt{34}}{34}\)
\(S_{ABC}=\dfrac{1}{2}\cdot2\cdot\sqrt{34}\cdot\dfrac{5}{\sqrt{34}}=5\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2020
Câu 1:
Gọi G là trọng tâm tam giác \(\Rightarrow G\left(1;1\right)\)
\(\overrightarrow{BC}=\left(1;4\right)\Rightarrow\) đường thẳng d nhận \(\left(1;4\right)\) là 1 vtpt
Phương trình d:
\(1\left(x-1\right)+4\left(y-1\right)=0\Leftrightarrow x+4y-5=0\)
Câu 2:
Có 2 trường hợp thỏa mãn:
- Đường thẳng đi qua M và trung điểm AB
- Đường thẳng qua M và song song AB
TH1:
Gọi N là trung điểm AB \(\Rightarrow N\left(-1;2\right)\Rightarrow\overrightarrow{MN}=\left(-11;0\right)\)
\(\Rightarrow\) Đường thẳng MN nhận \(\left(0;1\right)\) là 1 vtpt
Phương trình MN:
\(0\left(x-10\right)+1\left(y-2\right)=0\Leftrightarrow y-2=0\)
TH2: \(\overrightarrow{AB}=\left(-8;4\right)=-4\left(2;-1\right)\)
Đường thẳng d song song AB nên nhận \(\left(1;2\right)\) là 1 vtpt
Phương trình d:
\(1\left(x-10\right)+2\left(y-2\right)=0\Leftrightarrow x+2y-14=0\)
CD
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 11 2019
\(\overrightarrow{AB}=\left(-4;3\right)\Rightarrow AB=\sqrt{4^2+3^2}=5\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 5 2021
\(\overrightarrow{AB}=\left(6;-2\right)\Rightarrow AB=2\sqrt{10}\)
Gọi I là trung điểm AB \(\Rightarrow I\left(1;4\right)\)
ĐƯờng tròn (C) nhận I là tâm và có bán kính \(R=\dfrac{AB}{2}=\sqrt{10}\)
Phương trình: \(\left(x-1\right)^2+\left(y-4\right)^2=10\)
AS
0
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2020
\(\overrightarrow{AB}=\left(2;4\right);\overrightarrow{AC}=\left(11;-2\right);\overrightarrow{BC}=\left(9;-6\right)\)
\(\Rightarrow AB=2\sqrt{5};AC=5\sqrt{5};BC=3\sqrt{13}\)
Gọi D là chân đường phân giác trong góc A trên BC
\(\frac{DB}{DC}=\frac{AB}{AC}=\frac{2}{5}\Rightarrow BD=\frac{2}{5}CD=\frac{2}{7}BC\Rightarrow\overrightarrow{BD}=\frac{2}{7}\left(9;-6\right)\)
\(\Rightarrow D\left(\frac{46}{7};\frac{44}{7}\right)\Rightarrow\overrightarrow{AD}=\left(\frac{32}{7};\frac{16}{7}\right)=\frac{16}{7}\left(2;1\right)\)
\(\Rightarrow\) Đường thẳng AD nhận \(\left(1;-2\right)\) là 1 vtpt
Phương trình AD:
\(1\left(x-2\right)-2\left(y-4\right)=0\Leftrightarrow x-2y+6=0\)
2.
Đường thẳng d có 1 vtpt là \(\left(1;3\right)\)
Gọi vtpt của d' là \(\left(a;b\right)\Rightarrow cos45^0=\frac{\left|a+3b\right|}{\sqrt{10\left(a^2+b^2\right)}}=\frac{1}{\sqrt{2}}\)
\(\Leftrightarrow a^2+6ab+9b^2=5a^2+5b^2\)
\(\Leftrightarrow4a^2-6ab-4b^2=0\Leftrightarrow\left(2a+b\right)\left(a-2b\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}b=-2a\\a=2b\end{matrix}\right.\)
Chọn \(a=2\Rightarrow\left[{}\begin{matrix}b=-4\\b=1\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}1\left(x+2\right)-2\left(y-0\right)=0\\2\left(x+2\right)+1\left(y-0\right)=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x-2y+2=0\\2x+y+4=0\end{matrix}\right.\)
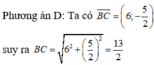
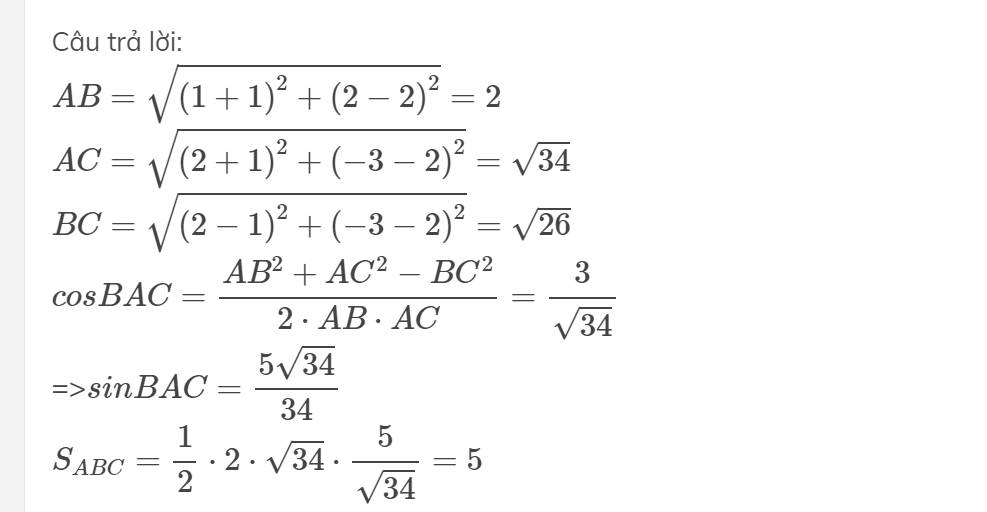
gọi M có tọa độ là (x;y) do M thuộc Ox=> tọa ddoooj M là (x;0)
ta có : \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\left(-2-X;5\right)+\left(3-X;-1\right)+\left(7-X;1\right)\right|\)
=\(\left|\sqrt{\left(-2-X\right)^2+5^2}+\sqrt{\left(3-X\right)^2+1}+\sqrt{\left(7-X\right)^2+1}\right|\)
=> BẠN TÌ gtnn CÁI TRONG LÀ ĐC
tìm gtnn giúp mik lun dc ko