Cho một thấu kính làm bằng thuỷ tinh (n = 1,5), một mặt lồi bán kính 10cm, một mặt lõm bán
kính 20cm. Một vật sáng AB = 2cm đặt thẳng góc với trục chính và cách thấu kính một khoảng d.
Xác định vị trí, tính chất, độ lớn và vẽ ảnh trong các trường hợp:
a) d = 60cm
b) d = 40cm
c) d = 20cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức tính tiêu cự của thấu kính:

Mặt khác, áp dụng công thức về vị trí ảnh – vật:
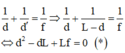
a) Để bài toán có nghiệm thì (*) phải có nghiệm, tức là:
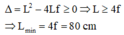
b) Trường hợp L= 90cm, khi đó (*) suy ra:


Tiêu cự của thấu kính phẳng lõm:
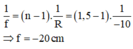
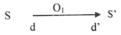
a) Ta có sơ đồ tạo ảnh qua thấu kính phẳng lõm:
Trường hợp 1: Ảnh S' là ảnh thật: d' = 12 cm
Suy ra khoảng cách từ S đến thấu kính:

Suy ra khoảng cách từ S đến thấu kính
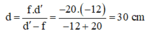
b) Giữ cố định S và thấu kính. Đổ một lớp chất lỏng vào mặt lõm. Ta được hệ hai thấu kính ghép sát là thấu kính phẳng lõm tiêu cự 20 cm và thấu kính phẳng lồi, chiết suất n'
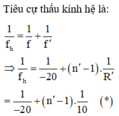
Bây giờ ảnh cuối cùng của S nằm cách thấu kính 20cm. Ta xét hai trường hợp:
Trường hợp 1: Ảnh S' là ảnh thật: d' = 20 cm
Ta có:
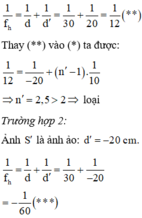
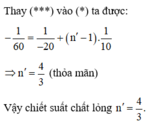

Đáp án cần chọn là: C
Ta có:
1 f = n − 1 1 R 1 + 1 R 2
= 1,5 − 1 1 10 + 1 ∞ = 1 20
→ f = 20 c m
+ Tiêu cự của thấu kính:
+ Vì ảnh hứng trên màn là ảnh thật nên d ' > 0 → L = d + d ' (1)
+ 1 f = 1 d + 1 d ' → d = d ' f d ' − f (2)
Thế (2) vào (1), ta được:
↔ L d ' − f = d ' 2 ↔ d ' 2 − L + f L = 0 (3)
Vì trên màn thu được ảnh rõ nét nên phương trình (3) phải có nghiệm hay Δ ≥ 0
Δ = b 2 − 4 a c = L 2 − 4 f L ≥ 0
→ L ≥ 4 f → L min = 4 f = 4.20 = 80 c m

Đáp án A
Thấu kính hai mặt lõm trong không khí là thấu kính phân kì:
Ta có
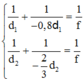
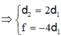
Mặt khác
![]()
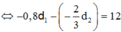

![]()
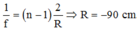

Ta có
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{df}{d-f}=-10cm< 0\)
Ảnh là ảnh ảo và cách thấu kính 1 đoạn \(d'=10cm\)
\(\Rightarrow h'=20\times\dfrac{20}{10}=40cm\\ \Rightarrow h'=2h\)

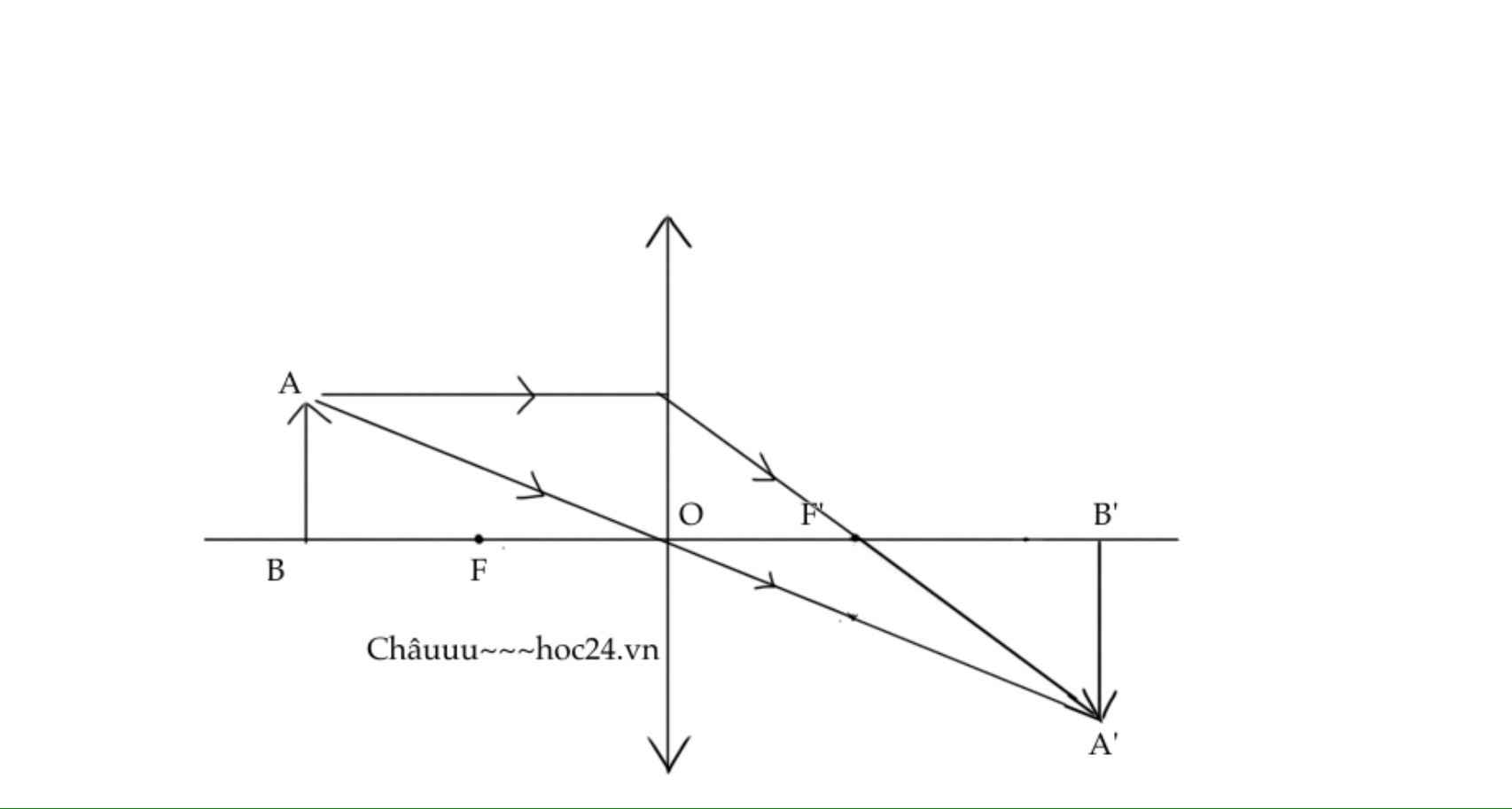
Sơ đồ tạo ảnh:

Áp dụng công thức về vị trí ảnh – vật:

Như vậy k > 0 nên ảnh cùng chiều với vật cao bằng một phần ba vật.


+ Hệ thấu kính bây giờ gồm thấu kính chất lỏng dạng phẳng - lồi và thấu kính thủy tinh dạng phẳng - lõm được ghép sát đồng trục với nhau.
+ Theo đề, ảnh S' là ảnh ảo và cách thấu kính tương đương 20 cm => d' = -20 (cm)
+ Vì vật được giữ cố định nên lúc này vật cách thấu kính tương đương d = 30 cm
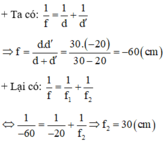
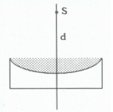


\(\frac{1}{f}=\left(n-1\right)\left(\frac{1}{R_1}+\frac{1}{R_2}\right)\) với R1 = 10 cm ; R2 = -20 cm → f = 40 cm
d' = 24 cm, ảnh thật cách thấu kính 24cm, ngược chiều vật và có độ lớn 1,2cm
b) d′=\(\infty\) : ảnh ở xa vô cùng.
c) d′=−40 < 0 : ảnh ảo ở sau thấu kính, cách thấu kính 40cm