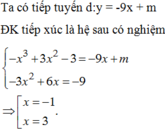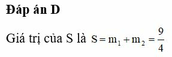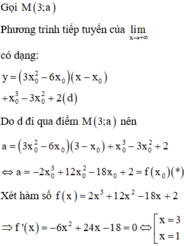Tìm trên đường thẳng y= -2 các điểm kẻ đến đồ thị hàm số y= x3-3x2+2 (C) hai tiếp tuyến vuông góc với nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi ![]() là tọa độ tiếp điểm và k là hệ số góc của tiếp tuyến.
là tọa độ tiếp điểm và k là hệ số góc của tiếp tuyến.
Theo giả thiết, ta có 
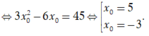
Với 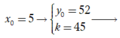 Phương trình tiếp tuyến: y = 45x - 173
Phương trình tiếp tuyến: y = 45x - 173

Chọn D.
Kí hiệu d là tiếp tuyến của đồ thị hàm số và (x0;y0) là tọa độ của tiếp điểm.
Ta có: d vuông góc với đường thẳng y =
-
1
45
x
+
2018
nên 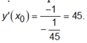
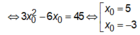
Với ![]() => phương trình tiếp tuyến của đồ thị là: y = 45(x-5) + 52 = 45x - 173
=> phương trình tiếp tuyến của đồ thị là: y = 45(x-5) + 52 = 45x - 173
Với ![]() => phương trình tiếp tuyến của đồ thị là: y = 45(x+3) - 52 = 45x + 83
=> phương trình tiếp tuyến của đồ thị là: y = 45(x+3) - 52 = 45x + 83

Phương trình hoành độ giao điểm của hai đồ thị:
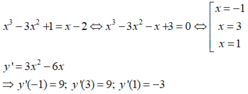
Ba tiếp tuyến tại giao điểm của đồ thị hàm số với đường thẳng y = x - 2 có tổng các hệ số góc là: 9 + 9 + (-3) = 15.
Chọn A.

Phương pháp:
+) Giải phương trình hoành độ giao điểm, tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Xét phương trình hoành độ giao điểm của hai đồ thị hàm số:


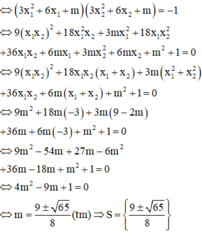
Vậy tổng các phần tử của tập hợp S bằng 9 4
Chọn: C