Một con lắc lò xo dao động với tần số góc 20rad/s. Tại thời điểm t1 và t2 = t1 +Δt, vật có thế năng (mốc ở VTCB ) bằng bốn lần động năng. Gía trị nhỏ nhất của Δt?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
19 tháng 6 2017
Chọn A
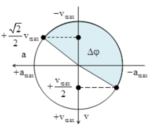
+ Với hai đại lượng vuông pha a và v, ta có phương trình độc lập:
+ Với hai thời điểm t1 và t2 ta có hệ:
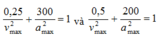
=> ω = 20 rad/s và vmax = 100 cm/s.
+ Từ hình vẽ xác định được khoảng thời gian tương ứng là:
VT
24 tháng 11 2018
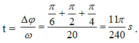
Chọn đáp án C
Tại t = t 2 thì:
W đ 2 = W t 2 = 0,064 J => W = 0,128 J.
Tại t 1 = 0 thì:
W đ 1 = 0,096 J => W t 1 = 0,032 J.
W t W = x a 2 ⇒ x = ± A W t W .
Áp dụng vào hai thời điểm
=> x 1 = ± A 2 . và x 2 = ± A 2 .
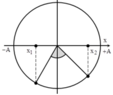
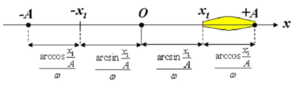
Theo bài ra, từ t 1 đến t 2 thì động năng tăng đến giá trị cực đại rồi giảm, tức thế năng của con lắc giảm đến 0 rồi tăng, tương ứng với vật đi từ vị trí x 1 = A 2 . qua vị trí cân bằng, đến x 2 = - A 2 . hoặc ngược lại.
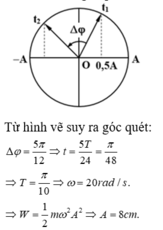
Ta xét 1 trường hợp như trên hình vẽ.
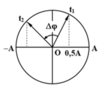
Từ hình vẽ suy ra góc quét:
Δ φ = 5 π 12 ⇒ t = 5 T 24 = π 48
⇒ T = π 10 ⇒ ω = 20 r a d / s
⇒ W = 1 2 m ω 2 A 2 ⇒ A = 8 c m .
VT
11 tháng 2 2018
Đáp án C
Cơ năng của con lắc E = E d 2 + E t 2 = 0 , 128 J
→ Biểu diễ dao động của vật tương ứng trên đường tròn.
+ Từ hình vẽ ta có Δ t = T 360 a r sin − 0 , 5 A A + a r sin 2 A 2 A = π 48
→ T = 0,1π → ω = 20 rad/s
Vậy biên độ dao động của con lắc là A = 2 E m ω 2 = 2.0 , 128 0 , 1.20 2 = 8 c m
VT
22 tháng 11 2017
Đáp án C.
Sử dụng mối quan hệ giữa dao động điều hòa và chuyển động tròn đều và các công thức về cơ năng, ta thấy:
Theo đề, tại thời điểm t 2 thì:
nên 
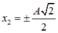và:
Tại 
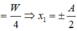
Như vậy, trong thời gian
π
48
s
vật đi từ vị trí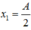 
qua vị trí cân bằng rồi đến vị trí 
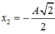, góc quay tương ứng là:
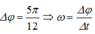
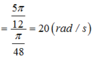
Và 
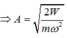
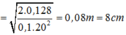
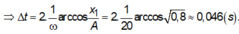
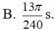
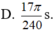
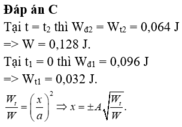
Bài này có vẻ lẻ quá bạn.
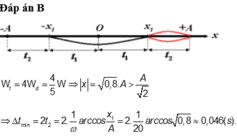
\(W_t=4W_đ\Rightarrow W_đ=\dfrac{W_t}{4}\)
Cơ năng: \(W=W_đ+W_t=W_t+\dfrac{W_t}{4}=\dfrac{5}{4}W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=\dfrac{5}{4}.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{2}{\sqrt 5}A\)
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(\cos\alpha=\dfrac{2}{\sqrt 5}\)\(\Rightarrow \alpha =26,6^0\)
Thời gian nhỏ nhất là: \(\Delta t=\dfrac{26,6\times 2}{360}.T=\dfrac{26,6\times 2}{360}.\dfrac{2\pi}{20}=0.046s\)
bạn ơi cho mình hỏi thời gian nhỏ nhất hay lớn nhất thì cách tính vẫn vậy hả?