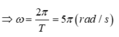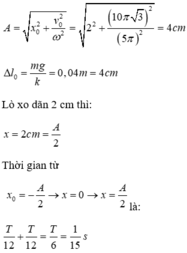Một con lắc đơn có l=20cm, g=9.8m/s^2. Kéo vật ra khỏi phương đứng 1 góc 0.1rad rồi truyền cho nó một vận tốc 14cm/s về VTCB. Chọn to=0 lúc vật đi qua VTCB lần 1 chiều dương trùng chiều kéo vật. Viết phương trình li độ dài và phương trình li độ góc. Nếu tăng góc lệch α lên 2 lần thì chu kì của con lắc thay đổi như thế nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chu kì dao động con lắc lò xo:
\(T=2\pi\cdot\sqrt{\dfrac{m}{k}}=2\pi\cdot\sqrt{\dfrac{0,4}{200}}=\dfrac{\pi\sqrt{5}}{25}\left(s\right)\)
Tần số góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{\pi\sqrt{5}}{25}}=10\sqrt{5}\left(rad\right)\)
Biên độ dao động:
\(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{2^2+\dfrac{\left(20\sqrt{2}\right)^2}{\left(10\sqrt{5}\right)^2}}=\dfrac{2\sqrt{35}}{5}\approx2,4\left(cm\right)\)
Gốc thời gian là lúc vật ở VTCB nên \(\varphi_0=0\)
PT dao động:
\(x=Acos\left(\omega t+\varphi_0\right)=2,4cos\left(10\sqrt{5}t\right)\) (cm)

Nếu b biết giải bài này thì chỗ kia là hợp với phương thẳng đứng 40 độ nha.

\(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,25}}=20\) (rad/s)
Độ dãn tại VTCB:
\(\Delta l=\dfrac{mg}{k}=\dfrac{0,25\cdot10}{100}=0,025m=2,5cm\)
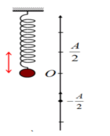
Lò xo kéo xuống dưới giãn 7,5cm.
\(\Rightarrow\)Biên độ: \(A=7,5-2,5=5cm=0,05m\)
Tại thời điểm ban đầu \(t=0\): \(x=-A\)\(\Rightarrow\varphi=\pi\)
Vậy pt là \(x=5cos\left(20t+\pi\right)cm\)
\(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,25}}=20\) (rad/s)
\(F_k=P\Rightarrow\Delta l.k=mg\Rightarrow\Delta l=\dfrac{mg}{k}=\dfrac{0,25.10}{100}=0,025\left(m\right)\)
Ta có : \(A+\Delta l=7,5\left(cm\right)\) \(\Rightarrow A=7,5-2,5=5\left(cm\right)\)
Trục Ox thẳng đứng ; chiều (+) hướng lên ; gốc tọa độ ở VTCB t0 = 0 lúc thả vật \(\Rightarrow\varphi=-\pi\)
Phương trình dao động là : \(x=5.cos\left(20t-\pi\right)\)