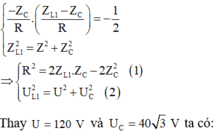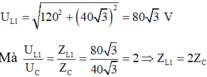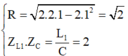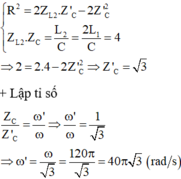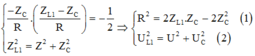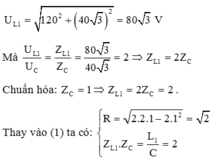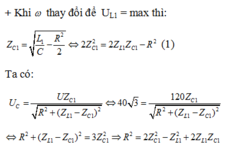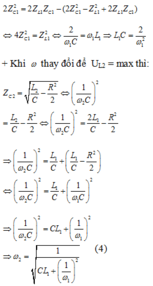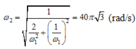Cho mạch điện xoay chiều gồm RLC nối tiếp, L biến thiên. Đặt vào 2 đầu mạch điện hiều điện thế xoay chiều\(u=120\sqrt{2}cos\left(\omega t\right)V\). Trong đó \(\omega\) thay đổi được. Cố định L=L1 thay đổi \(\omega\) thấy khi \(\omega\) =120\(\pi\) (rad/s) thì \(_{U_L}\) max khi đó \(_{U_c}\) =\(40\sqrt{3}\) V. Sau đó cố định L=L2=2L1 thay đổi \(\omega\), giá trị của \(\omega\) để \(U_L\) max
\(A.40\pi\sqrt{3}\)
\(B.100\pi\)
\(C.120\pi\sqrt{3}\)
\(D.60\pi\)