Vẽ góc xOy bằng 60'. Vẽ góc yOz kề bù với góc xOy; Vẽ tia Ot là tia đối của Oy.
a.Tính số đo các góc yOz; góc zOt?
b. Vẽ Om là tia phân giác của góc zOy; Vẽ On là tia phân giác của góc zOt,tính ố đo góc mOn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2017
a) Ta có: xOy+ yOz=180
60 + yOz=180
=> yOz=180-60=120
b) Om, On là tia thì làm gì có độ dài cố định chứ bạn, đáng lẽ là tính góc mOn chứ
16 tháng 5 2017
Còn nếu đề là tính mOn thì tính như sau:
Ta có: mOy= 1/2.xOy
yOn= 1/2.yOz
=> mOn = mOy+yOn = 1/2 xOy + 1/2 yOz
= 1/2(xOy+yOz)
=1/2 . 180
=90
A
2
KV
28 tháng 9 2023
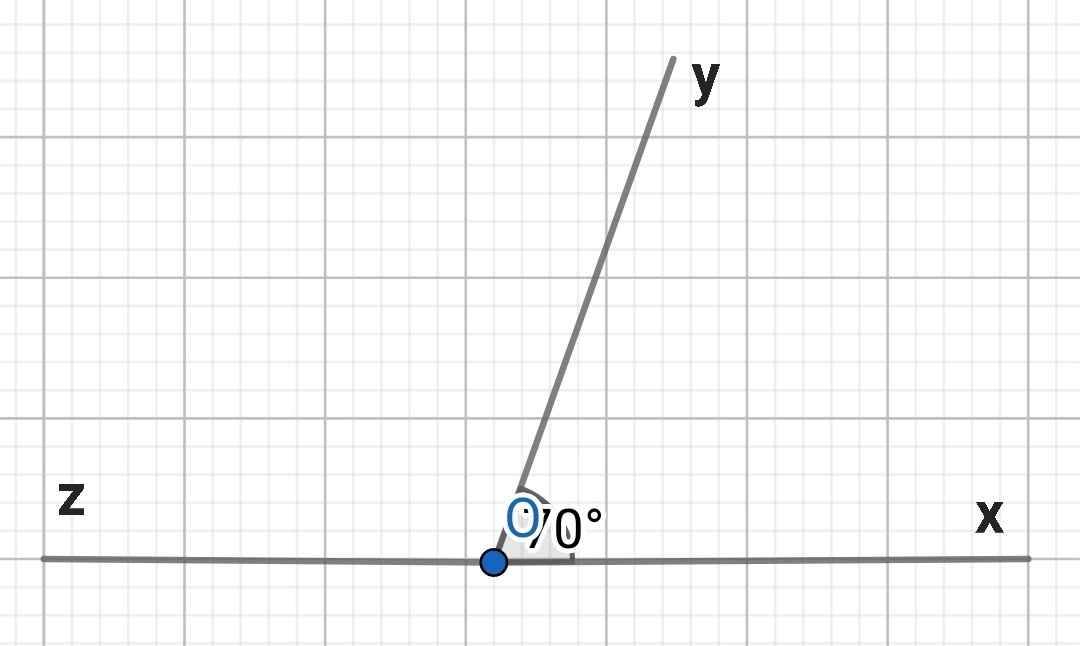Ta có:
∠xOy + ∠yOz = 180⁰ (kề bù)
⇒ ∠yOz = 180⁰ - ∠xOy
= 180⁰ - 70⁰
= 110⁰
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 12 2023
Vì góc yOz và góc xOy là hai góc kề bù nên Oz và Ox cùng nằm trên một đường thẳng zx (1)
Tương tự ta có: Ot và Oy cùng nằm trên một đường thẳng
\(\widehat{xOt}\) và \(\widehat{yOz}\) là hai góc đối đỉnh
⇒ \(\widehat{O_2}\) = \(\dfrac{1}{2}\) \(\widehat{xOt}\) = \(\dfrac{1}{2}\) \(\widehat{yOz}\) = \(\widehat{O_5}\)
Mặt khác ta có: \(\widehat{O_2}\) + \(\widehat{O_1}\) + \(\widehat{O_6}\) = 1800 (gt)
⇒ \(\widehat{O_1}\) + \(\widehat{O_6}\) + \(\widehat{O_5}\) = 1800
⇒ Om và On cùng thuộc một đường thẳng mn (2)
Kết hợp (1) và (2) ta có: góc zOn và góc xOm là hai góc đối đỉnh
R2
19 tháng 3 2020
có góc xOy+ góc yOz = 180 độ ( 2 góc kề bù)
mà góc xOy = 30 độ (gt)
=> góc yOz=180 độ - 30 độ = 150 độ
Có góc zOt + góc tOy = góc yOz
mà góc yOz = 150 độ (cmt)
góc zOt= 60 độ (gt)
=> 60 độ + góc tOy= 150 độ
=> góc tOy = 150độ - 60 độ = 90 độ
=> Ot vuông góc vs Oy
vậy đường thẳng chứa tia Ot và đường thẳng chứa tia Oy vuông góc vs nhau
Hình cậu tự vẽ
11 tháng 6 2021
a)Vì góc xOy và góc yOz là 2 góc kề bù
suy ra:xOy +yOz =180\(^0\)
thay xOy =60\(^0\) có:
60 \(^0\)+yOz =180\(^0\)
yOz =180\(^0\)-60\(^0\)
yOz =120\(^0\)
Vậy yOz=120\(^0\)
b)Vì Ot là tia phân giác của góc xOy
suy ra:xOt=tOy=xOy:2=60\(^0\):2=30\(^0\)(thay xOy=60\(^0\))
Vì Oy nằm giữa 2 tia Ot và Oz
suy ra:tOy+yOz=zOt
thay tOy=30\(^0\);yOz=120\(^0\)
30\(^0\)+120\(^0\) =zOt
150\(^0\) =zOt
Vậy zOt= 150\(^0\)
11 tháng 6 2021
Ta có: ∠yOz + ∠xOy = 180\(^0\) ( hai góc kề bù )
∠yOz + 60\(^0\) = 180\(^0\)
∠yOz = 120\(^0\) (1)
Ta có: ∠yOt = \(\dfrac{60^0}{2}\) = \(30^0\) ( vì Ot là phân giác ∠xOy ) (2)
TỪ (1) VÀ (2)
⇒ ∠yOz + ∠yOt = ∠zOt
120\(^0\) + \(30^0\) = ∠zOt
\(150^0\)= ∠zOt
Vậy ∠zOt = \(150^0\)
CM
28 tháng 8 2019
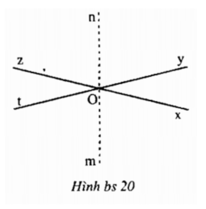
Vì góc yOz kề bù với góc xOy nên Oz là tia đối của tia Ox. Tương tự, góc xOt kề bù với góc xOy nên Ot là tia đối của tia Oy. Từ đó, hai góc zOy và tOx là hai góc đối đỉnh nên ∠zOy = ∠tOx.
Vì On, Om lần lượt là tia phân giác của góc zOy, góc xOt và ∠zOy = ∠tOx nên ∠zOn = ∠nOy = ∠xOm = ∠mOt.
Lại vì ∠zOn + ∠nOx = 180°,
Nên ∠mOx + ∠nOx = 180° hay ∠mOn = 180º.
Suy ra Om và On là hai tia đối nhau.
Từ đó, hai góc ∠zOn và ∠mOx là hai góc đối đỉnh.
HN
28 tháng 8 2021
O y t x z' t'
Cặp góc kề bù trong hình vẽ: \(\widehat{xOy};\widehat{zOy}\)
2,
Ot là tia phân giác \(\widehat{xOy}\Rightarrow\widehat{xOt}=\widehat{tOy}=\widehat{xOy}:2=100^o:2=50^o\)
Vì \(\widehat{zOy}\)kề bù \(\widehat{xOy}\Rightarrow\widehat{zOy}+\widehat{xOy}=180^o\Rightarrow\widehat{zoy}+100^o=180^o\Rightarrow\widehat{zOy}=80^o\)
Vì Ot' là tia phân giác \(\widehat{zOy}\Rightarrow\widehat{t'Oy}=\widehat{t'Oz}=\widehat{zOy}:2\Rightarrow80^o:2=40^o\)
Vì Oz và Ox đối nhau => tia Oy nằm giữa Oz; Ox => Oy cũng nằm giữa Ot; Ot'
\(\Rightarrow\widehat{t'Oy}+\widehat{tOy}=\widehat{tOt'}\Rightarrow40^o+50^o=\widehat{tOt'}\Rightarrow\widehat{tOt'}=90^o\)
a) Do yOz kề bù với xOy => xOz=180'
Ta có: xoy= 60' ; xoz=180'
=> xOy< xOz => Oy nằm giữa Oz; Ox
=> xOy+yOz=xOz
=>yOz=xOz-xOy
=180'-60'
=120'
Do Ot là tia đối của Oy nên chúng tạo thành một góc bẹt có tổng số đo là 180’
Ta có: yOz=120’; yOt=180’
=>yOz< yOt =>Oz nằm giữa Ot; Oy
=>yOz + zOt=yOt
=>zOt=yOt – yOz
=180’ – 120’
=60’
b) Vì Om là tia phân giác của zOy
=>yOm = mOz=yOz/2
=120’: 2
= 60’
Vì On là tia phân giác của zOt
=>zOn= nOt= zOt/2
=60’:2
=30’
Vì Oz nằm giữa Oy; Ot
=>Oz nằm giữa Om; On
=>mOz+zOn=mOn
=>mOn= 60’+30’
=90’
Đó là ý kiến của mk bạn có thể tham khảo
( mà mk ko viết đc kí hiệu góc bn bỏ qua nhé)
60 độ nhé