cho tam giác abc vuông tại a k là trung điểm của bc . TỪ I kẻ IE vuông góc với AB , kẻ IF vuông góc với AC tại F trên tia IE lấy điểm M sao cho EM = EI trên tia IF lấy điểm M sao cho FI = FN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2019
a ) Xét ◇DENF có :
Góc N = Góc F = Ê = 90°
⇒◇DENF là hình chữ nhật
b ) Trong ΔMNP có : ND là đường trung tuyến
⇒ND = DP ( vì đường trung tuyến bằng nữa cạnh huyền )
Xét ΔNDF và ΔPDF có :
- ND = DP ( cmt )
- Góc NFD = Góc PFD ( = 90° )
- DF : cạnh chung
⇒ΔNDF = ΔPDF ( cạnh huyền - cạnh góc vuông )
⇒NF = PF ( 2 cạnh tương ứng )
⇒F là trung điểm NP
KV
27 tháng 10 2023
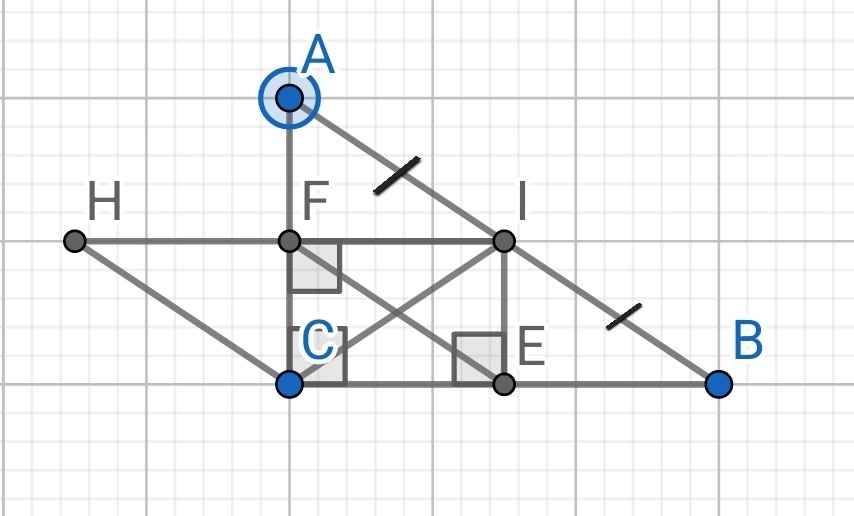*) Tứ giác CEIF là hình gì?
Tứ giác CEIF có:
∠CEI = ∠CFI = ∠ECF = 90⁰ (gt)
⇒ CEIF là hình chữ nhật
*) Do CEIF là hình chữ nhật (cmt)
⇒ FI = CE và FI // CE
Do FI // CE (cmt)
⇒ FH // CE
Do FI = CE (cmt)
FI = FH (gt)
⇒ FH = CE
Tứ giác CHFE có:
FH // CE (cmt)
FH = CE (cmt)
⇒ CHFE là hình bình hành
27 tháng 10 2023
Sửa đề: IF vuông góc AC tại F
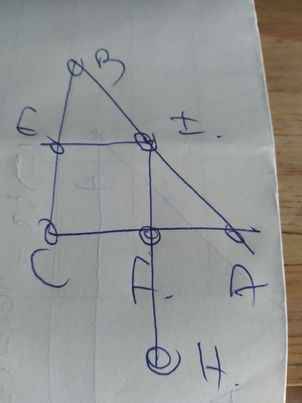
a: Xét tứ giác CEIF có
\(\widehat{CEI}=\widehat{CFI}=\widehat{FCE}=90^0\)
Do đó: CEIF là hình chữ nhật
b: CEIF là hình chữ nhật
=>CE//FI và CE=FI
CE=FI
FI=FH
Do đó: CE=FH
CE//FI
\(F\in IH\)
Do đó: CE=FH
Xét tứ giác CEFH có
CE//FH
CE=FH
Do đó: CEFH là hình bình hành
20 tháng 2 2023
a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
b: Xét tứ giác BECF có
I là trung điểm chung củaBC và EF
=>BECF là hình bình hành
=>BE//CF
=>CF vuông góc FI
20 tháng 2 2023
a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
b: Xét tứ giác BECF có
I là trung điểm chung củaBC và EF
=>BECF là hình bình hành
=>BE//CF
=>CF vuông góc FI
15 tháng 4 2023
1: Xét ΔCBD có CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
=>CA là phân giác của góc BCD
2: Xét ΔCEI vuông tại E và ΔCFI vuông tại F có
CI chung
góc ECI=góc FCI
=>ΔCEI=ΔCFI
=>CE=CF
Xét ΔCBD có CE/CD=CF/CB
nên EF//BD
3: IE=IF
IF<IB
=>IE<IB
26 tháng 2 2023
a: Xét ΔAHB vuông tại H và ΔAHE vuông tại H có
AH chung
HB=HE
=>ΔAHB=ΔAHE
b: Xét tứ giác AECF có
I là trung điểm chung của AC và EF
=>AECF là hình bình hành
=>AF//EC
=>AF vuông góc AH
c: AECF là hình bình hành
=>CF=AE>HA
13 tháng 7 2023
a: Xét ΔABH vuông tại H và ΔKIH vuông tại H có
HA=HK
HB=HI
=>ΔABH=ΔKIH
b: ΔABH=ΔKIH
=>góc ABH=góc KIH
=>AB//IK
c: IK//AB
AB vuông góc AC
=>IK vuông góc AC
=>I,K,E thẳng hàng
d: Xét tứ giác ABKI có
H là trung điểm chung của AK và BI
AK vuông góc BI
=>ABKI là hình thoi
=>AB=AI=IK
=>IK=ID
=>góc IKD=góc IDK