Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) Xét ◇DENF có :
Góc N = Góc F = Ê = 90°
⇒◇DENF là hình chữ nhật
b ) Trong ΔMNP có : ND là đường trung tuyến
⇒ND = DP ( vì đường trung tuyến bằng nữa cạnh huyền )
Xét ΔNDF và ΔPDF có :
- ND = DP ( cmt )
- Góc NFD = Góc PFD ( = 90° )
- DF : cạnh chung
⇒ΔNDF = ΔPDF ( cạnh huyền - cạnh góc vuông )
⇒NF = PF ( 2 cạnh tương ứng )
⇒F là trung điểm NP

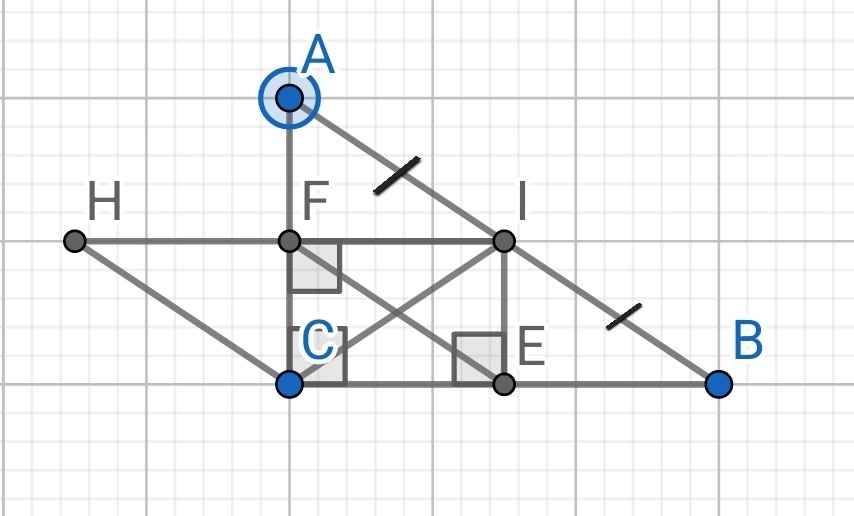 *) Tứ giác CEIF là hình gì?
*) Tứ giác CEIF là hình gì?
Tứ giác CEIF có:
∠CEI = ∠CFI = ∠ECF = 90⁰ (gt)
⇒ CEIF là hình chữ nhật
*) Do CEIF là hình chữ nhật (cmt)
⇒ FI = CE và FI // CE
Do FI // CE (cmt)
⇒ FH // CE
Do FI = CE (cmt)
FI = FH (gt)
⇒ FH = CE
Tứ giác CHFE có:
FH // CE (cmt)
FH = CE (cmt)
⇒ CHFE là hình bình hành
Sửa đề: IF vuông góc AC tại F
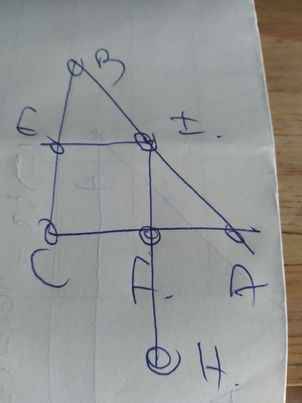
a: Xét tứ giác CEIF có
\(\widehat{CEI}=\widehat{CFI}=\widehat{FCE}=90^0\)
Do đó: CEIF là hình chữ nhật
b: CEIF là hình chữ nhật
=>CE//FI và CE=FI
CE=FI
FI=FH
Do đó: CE=FH
CE//FI
\(F\in IH\)
Do đó: CE=FH
Xét tứ giác CEFH có
CE//FH
CE=FH
Do đó: CEFH là hình bình hành

d: Xét ΔAIM có
AB là đường cao
AB là đường trung tuyến
DO đó: ΔAIM cân tại A
mà AB là đường trung tuyến
nên AB là phân giác của góc IAM(1)
Xét ΔAIN có
AC là đường cao
AC là đường trung tuyến
Do đó: ΔAIN cân tại A
mà AC là đường cao
nên AC là tia phân giác của góc NAI(2)
Từ (1) và (2) suy ra \(\widehat{MAN}=2\cdot90^0=180^0\)
=>M,A,N thẳng hàng
mà AN=AM
nên A là trung điểm của NM

a: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Hình bình hành ABCD có \(\widehat{BAD}=90^0\)
nên ABCD là hình chữ nhật
b: ABCD là hình chữ nhật
=>AD//BC và AD=BC
AD=BC
AD=DE
Do đó: DE=CB
Xét tứ giác EDBC có
ED//BC
ED=BC
Do đó: EDBC là hình bình hành
=>EB cắt DC tại trung điểm của mỗi đường
=>I là trung điểm của EB
=>IE=IB
c: Xét ΔACK có
H,M lần lượt là trung điểm của AK,AC
=>HM là đường trung bình
=>HM//CK
=>CK//BD
Xét ΔDAK có
DH là đường cao, là đường trung tuyến
Do đó: ΔDAK cân tại D
=>DA=DK
mà DA=BC
nên DK=BC
Xét tứ giác BKCD có CK//BD
nên BKCD là hình thang
mà BC=KD
nên BKCD là hình thang cân

a) Do O là trọng tâm giác tam giác ABC nên \(OE=\frac{1}{2}OC\)
Lại có \(OE=\frac{1}{2}OK\) (Do EK = EO)
Vậy nên OC = OK.
Tương tự OI = OB. Vậy tứ giác BKIC là hình bình hành.
Lại có do tam giác ABC cân tại A nên AO là đường trung trực của BC. Vậy thì OB = OC hay ta suy ra BI = CK
Hình bình hành BKIC có hai đường chéo bằng nhau nên nó là hình chữ nhật.
b) Xét tứ giác BKAO có EK = EO, EA = EB nên BKAO là hình bình hành.
Do BKIC là hình chữ nhật nên OB = OI
Vậy nên AK song song và bằng OI hay AIOK là hình bình hành.
Ta cũng có OK = OI nên AIOK là hình thoi.
c) Gọi J là trung điểm của NC.
Xét tam giác BNC có M là trung điểm BC, J là trung điểm NC nên MJ là đường trung bình hay MJ // BN.
Xét tam giác MNC có MD = ND; NJ = JC nên DJ là đường trung bình hay DJ // MC.
Do \(MC\perp OM\Rightarrow JD\perp OM\)
Xét tam giác OMJ có \(JD\perp OM;MN\perp OJ\) nên D là trực tâm tam giác.
Suy ra \(OD\perp MJ\)
Mà MJ // NB nên \(NB\perp OD.\)

Sửa đề: \(FN=IN\)
a, Xét tứ giác \(AEIF\) có :
\(\widehat{E}=\widehat{F}=\widehat{A}=90^o\)
\(\rightarrow EAIF\) là hình chữ nhật ( Dấu hiệu nhận biết hcn)
b, Đề sai nhé

a: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Hình bình hành ABCD có \(\widehat{BAD}=90^0\)
nên ABCD là hình chữ nhật
b: ABCD là hình chữ nhật
=>AD//BC và AD=BC
AD//BC
D\(\in\)AE
Do đó: ED//BC
AD=BC
ED=DA
Do đó: BC=ED
Xét tứ giác EDBC có
ED//BC
ED=BC
Do đó: EDBC là hình bình hành
=>EB cắt DC tại trung điểm của mỗi đường
mà I là trung điểm của DC
nên I là trung điểm của EB
=>IE=IB
c: Xét ΔACK có
H,M lần lượt là trung điểm của AK,AC
=>HM là đường trung bình của ΔACK
=>HM//CK
=>CK//DB
Xét ΔDAK có
DH là đường cao
DH là đường trung tuyến
Do đó:ΔDAK cân tại D
=>DA=DK
mà DA=BC(ABCD là hình chữ nhật)
nên DK=BC
Xét tứ giác BKCD có CK//BD
nên BKCD là hình thang
Hình thang BKCD có CB=DK
nên BKCD là hình thang cân