góc giữa hướng của hạt bay ra được tính bằng công thức gì
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
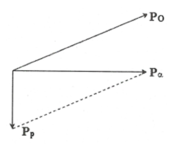
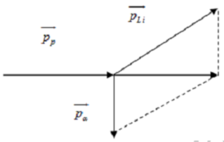
Theo định luật bảo toàn động lượng:
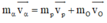
Các vectơ được biểu diễn trên hình vẽ. Từ đó ta có:
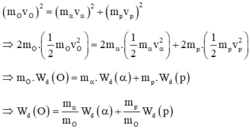
Theo định luật bảo toàn năng lượng:
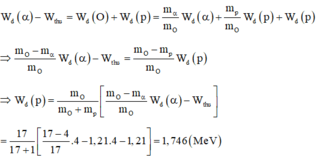

Đáp án B.
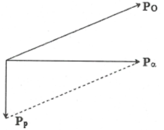
Theo định luật bảo toàn động lượng:
m α v α → = m p v p → + m 0 v o →
Các vectơ được biểu diễn trên hình vẽ. Từ đó ta có:
m o v o 2 = m α v α 2 + m p v p 2 ⇒ 2 m o . 1 2 m 0 . v 2 0 = 2 m α . 1 2 m α . v 2 α + 2 m p . 1 2 m p v 2 p ⇒ m o w d O = m α . w d α + m p . w d P ⇒ w d O = m α m o w d α + m p m o w d P
Theo định luật bảo toàn năng lượng:
w d α - w t h u = w d O + w d P = m α m o w d α + m p m o w d ( P ) + w d P ⇒ m o - m α m o w d α - w t h u = m o - m p m o w d P ⇒ w d P = m 0 m 0 + m p = m o - m α m o w d α - w t h u = 17 17 + 1 17 - 4 17 . 4 - 1 , 21 . 4 - 1 , 21 = 1 , 746 ( M e v )

Phương pháp: Sử dụng định luật bảo toàn động lượng.
Cách giải: Ta có thể biểu diễn các vecto động lượng như hình vẽ:
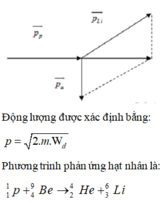
Áp dụng định luật bảo toàn động lượng cho hệ hai hạt p và Be.
![]()
Gọi góc giữa vec to động lượng của Li và vecto tổng động lượng là α. Ta có
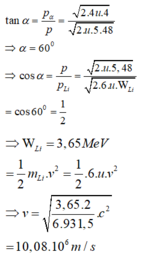
Đáp án A

Đáp án A
Phương pháp: Sử dụng định luật bảo toàn động lượng.
Cách giải: Ta có thể biểu diễn các vecto động lượng như hình vẽ:
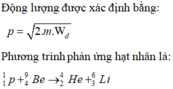
Áp dụng định luật bảo toàn động lượng cho hệ hai hạt p và Be.
![]()
Gọi góc giữa vec to động lượng của Li và vecto tổng động lượng là α. Ta có
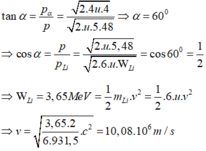
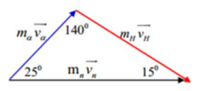
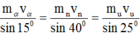
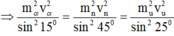
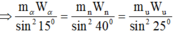
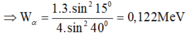
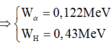


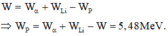
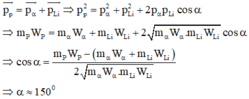
+ B1: Bạn dùng định luật bảo toàn động lượng \(\vec{p_{trước}}=\vec{p_{sau}}\)
+ B2: Bạn chuyển các véc tơ động lượng của các hạt muốn tính góc về 1 vế.
+ B3: Bạn bình phương 2 vế, sẽ xuất hiện cos góc giữa 2 hạt, và chuyển về biểu thức động năng rồi tính.