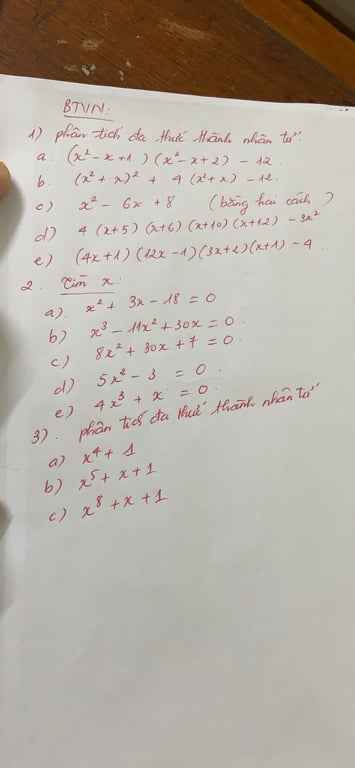
ai giải bài một và ba giúp mik đc hok ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 4xy3-2=2(2xy3-1)
b) 5xy3+2xy+4x2y2=xy(5y2+2+4xy)
d) 5x(x-y)-2y(y-x)=(5x+2y)(x-y)
e) x3-6x2+12x-8=(x-2)3
f) (x+1)(x+2)(x+3)(x+4)-3=\(\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]-3\)=\(\left(x^2+5x+4\right)\left(x^2+5x+6\right)-3\)
Đặt x2+5x+5=y
\(\left(x^2+5x+4\right)\left(x^2+5x+6\right)-3\)
= (y-1)(y+1)-3
=y2-1-3
=y2-4
=(y-2)(y+2)
= (x2+5x+5-2)(x2+5x+5+2)
= (x2+5x+3)(x2+5x+7)
h) 6x2-7x+1=(6x2-6x)-(x-1)=6x(x-1)-(x-1)=(6x-1)(x-1)


Bàu 68:
-Các t/c đó đc suy ra từ các định lý:
+a,b)định lý:Tổng ba góc của một tam giác bằng 180°
+c)đl:Trong một tam giác cân,hai góc ở đáy = nhau
+d)đl:Nếu một tam giác có hai góc =nhau thì tam giác đó là tam giác cân
HÙGHJUJNHJRJIJKJHJUIRGJUIJUIGJUIGJUIFKJIOJUITJUIKIOUJRJUIGJUTRGJUI6JUHJUIHJYUIJUIGJUIJUIRIGIJUIERGJU6JIGJUIJUITGHJUTJUIHITGJUIYIJH

May 1 bộ hết số mét vải là:
27 : 5 = 5,4 (m)
May 16 bộ quần áo hết số mét vải là:
5,4 x 16 = 86,4 (m)
Đáp số: 86,4 m vải

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40
Bài 3:
a) \(x^4+4\)
\(=x^4+4x^2+4-4x^2\)
\(=\left(x^2+2\right)^2-\left(2x\right)^2\)
\(=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
b) \(x^5+x+1\)
\(=x^5+x^4+x^3-x^4-x^3-x^2+x^2+x+1\)
\(=x^3\left(x^2+x+1\right)-x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^3-x^2+1\right)\)
c) \(x^8+x+1\)
\(=x^8+x^7+x^6-x^7-x^6-x^5+x^5+x^4+x^3-x^4-x^3-x^2+x^2+x+1\)
\(=x^6\left(x^2+x+1\right)-x^5\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^6-x^5+x^3-x^2+1\right)\)
Bài 1:
a) \(\left(x^2-x+1\right)\left(x^2-x+2\right)-12\)
\(=\left(x^2-x\right)^2+3\left(x^2-x\right)+2-12\)
\(=\left(x^2-x\right)^2+5\left(x^2-x\right)-2\left(x^2-x\right)-10\)
\(=\left(x^2-x\right)\left(x^2-x+5\right)-2\left(x^2-x+5\right)\)
\(=\left(x^2-x+5\right)\left(x^2-x-2\right)\)
\(=\left(x-2\right)\left(x+1\right)\left(x^2-x+5\right)\)
b) \(\left(x^2+x\right)^2+4\left(x^2+x\right)-12\)
\(=\left(x^2+x\right)^2+6\left(x^2+x\right)-2\left(x^2+x\right)-12\)
\(=\left(x^2+x+6\right)\left(x^2+x-2\right)\)
\(=\left(x+2\right)\left(x-1\right)\left(x^2+x+6\right)\)
c) \(x^2-6x+8\)
\(=x^2-6x+9-1\)
\(=\left(x-3\right)^2-1\)
\(=\left(x-4\right)\left(x-2\right)\)