Cho hàm số : \(y=x^4+mx^3-2x^2-3mx+1\) (1)
Xác định m để hàm số (1) có hai cực tiểu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Đồ thị hàm bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành khi và chỉ khi \(f\left(x\right)=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3+3x^2+mx+m-2=0\) có 3 nghiệm pb
\(\Leftrightarrow x^3+3x^2-2+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-2\right)+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+m-2=0\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}1-2+m-2\ne0\\\Delta'=1-\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow m< 3\)
2.
Pt hoành độ giao điểm:
\(\dfrac{2x-2}{x+1}=2x+m\)
\(\Rightarrow2x-2=\left(2x+m\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+mx+m+2=0\) (1)
d cắt (C) tại 2 điểm pb \(\Rightarrow\) (1) có 2 nghiệm pb
\(\Rightarrow\Delta=m^2-8\left(m+2\right)>0\Rightarrow\left[{}\begin{matrix}m>4+4\sqrt{2}\\m< 4-4\sqrt{2}\end{matrix}\right.\)
Khi đó, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{m}{2}\\x_Ax_B=\dfrac{m+2}{2}\end{matrix}\right.\)
\(y_A=2x_A+m\) ; \(y_B=2x_B+m\)
\(\Rightarrow AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2+\left(2x_A-2x_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2=1\)
\(\Leftrightarrow\left(x_A+x_B\right)^2-4x_Ax_B=1\)
\(\Leftrightarrow\left(-\dfrac{m}{2}\right)^2-4\left(\dfrac{m+2}{2}\right)=1\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10\\m=-2\end{matrix}\right.\)

- Khi \(m=0\Rightarrow y=x-1\) nên hàm số không có cực trị
- Khi \(m\ne0\Rightarrow y'=3mx^2+6mx-\left(m-1\right)\)
hàm số không có cực trị khi và chỉ chỉ y' = 0 không có nghiệm hoặc có nghiệm kép
\(\Leftrightarrow\Delta'=9m^2+3m\left(m-1\right)=12m^2-3m\le0\) \(\Leftrightarrow0\le m\)\(\le\frac{1}{4}\)

Đề đúng là \(y=mx^2+2\left(m^2-5\right)x^4+4\) chứ bạn (nghĩa là ko bị nhầm lẫn vị trí \(x^2\) và \(x^4\))
Hàm có đúng 2 điểm cực đại và 1 điểm cực tiểu khi:
\(\left\{{}\begin{matrix}2\left(m^2-5\right)< 0\\2\left(m^2-5\right).m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \sqrt{5}\)
\(\Rightarrow\) có 2 giá trị nguyên của m thỏa mãn

gợi ý :
Tìm giá trị của \(m\) để hàm số có cực đại ,cực tiểu .

ĐKXĐ
\(mx^4+mx^3+\left(m+1\right)x^2+mx+1\)
\(=\left(mx^4+mx^3+mx^2+mx\right)+\left(x^2+1\right)\)
=\(mx\left(x^3+x^2+x+1\right)+\left(x^2+1\right)\)
\(=mx\left(x+1\right)\left(x^2+1\right)+\left(x^2+1\right)\)
\(=\left(x^2+1\right).\left[mx\left(x+1\right)+1\right]>0\left(\forall x\right)\)
\(=>mx^2+mx+1>0\left(\forall x\right)\)
\(=>PT\hept{\begin{cases}mx^2+mx+1=0\left(zô\right)nghiệm\forall x\\m>0\end{cases}}\)
\(\hept{\begin{cases}\Delta< 0\\m>0\end{cases}=>\hept{\begin{cases}m^2-4m< 0\\m>0\end{cases}=>\hept{\begin{cases}m\left(m-4\right)< 0\\m>0\end{cases}=>0< m< 4}}}\)
=> m có 3 giá trị là 1,2,3 nha

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g\left(x\right)=f\left(x^2-2x\right)\)
\(g'\left(x\right)=2\left(x-1\right)f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
\(f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x^2-2x=-2\\x^2-2x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
BBT:
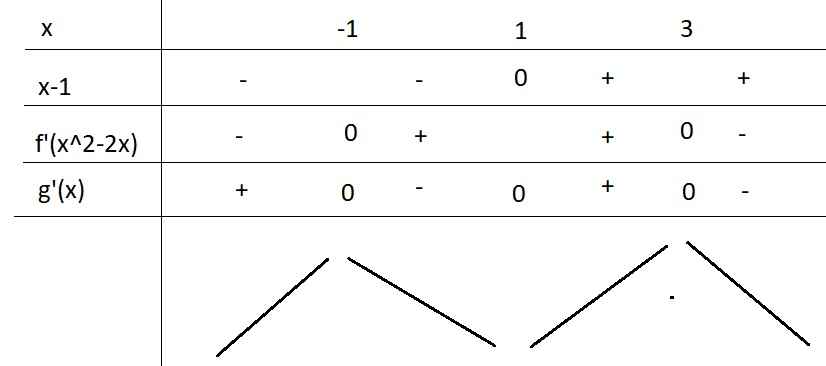
Từ BBT ta thấy \(f\left(x^2-2x\right)\) có 1 cực tiểu
\(y=x^4+mx^3-2x^2-2mx+1\) (1)
Đạo hàm \(y'=4x^2+3mx^2-4x-3m=\left(x-1\right)\left[4x^2+\left(4+3m\right)x+3m\right]\)
\(y'=0\) \(\Leftrightarrow\) \(\begin{cases}x=1\\4x^2+\left(4+3m\right)x+3m=0\left(2\right)\end{cases}\)
Hàm số có 2 cực tiểu \(\Leftrightarrow\) y có 3 cực trị \(\Leftrightarrow\)\(y'=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow\left(2\right)\) có 2 nghiệm phân biệt khác 1 \(\Leftrightarrow\) \(\begin{cases}\Delta=\left(3m-4\right)^2>0\\4+4+3m+3m\ne0\end{cases}\) \(\Leftrightarrow\) \(m\ne\pm\frac{4}{3}\)
Giả sử : Với \(m\ne\pm\frac{4}{3}\), thì \(y'=0\) có 3 nghiệm phân biệt \(x_1,x_2,x_3\)
Từ bảng biến thiên ta thấy hàm số có 2 cực tiểu
Kết luận : Vậy hàm số có 2 cực tiểu khi \(m\ne\pm\frac{4}{3}\)
\(\begin{cases}\frac{x_1+x_2}{2}=-2\\\frac{y_1+y_2}{2}=\frac{-2\left(x_1+x_2\right)+10}{2}=9\end{cases}\)
Tọa độ trung điểm cực đại và cực tiểu là (-2;9) không thuộc đường thẳng
\(y=\frac{1}{2}x\Rightarrow m=-3\) không thỏa mãn
Vậy m=1 thỏa mãn điều kiện đề bài