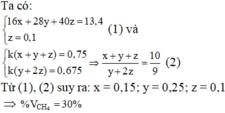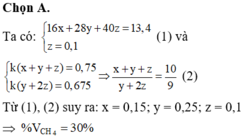Hỗn hợp X gồm metan, etilen, axetilen. Sục 7 gam X vào nước brom dư thì thấy có 48 gam brom pư. Cho 7 gam trên pư với AgNO3/NH3 dư trong NH3 thì thu được 24 gam kết tủa. Tính khối lượng mỗi chất trong X
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
Gọi x, y, z 1à số mol của CH4, C2H4 và C2H2 trong 8,6g hh X
=> 16x + 28y + 26z = 8,6 (1)
- Khi cho X td với dung dịch Br2 dư:
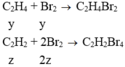
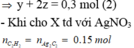


Ta có: \(n_X=\dfrac{10,08}{22,4}=0,45\left(mol\right)\)
\(n_{C_2Ag_2}=\dfrac{48}{240}=0,2\left(mol\right)=n_{C_2H_2}\)
\(\Rightarrow m_{C_2H_2}=0,2.26=5,2\left(g\right)\)
\(n_{Br_2}=\dfrac{88}{160}=0,55\left(mol\right)=n_{C_2H_4}+2n_{C_2H_2}\)
\(\Rightarrow n_{C_2H_4}=0,55-0,2.2=0,15\left(mol\right)\)
\(\Rightarrow m_{C_2H_4}=0,15.28=4,2\left(g\right)\)
\(\Rightarrow n_{CH_4}=0,45-0,15-0,2=0,1\left(mol\right)\)
\(\Rightarrow m_{CH_4}=0,1.16=1,6\left(g\right)\)

$C_2H_2 + 2AgNO_3 + 2NH_3 \to Ag_2C_2 + 2NH_4NO_3$
Theo PTHH :
n C2H2 = n Ag2C2 = 48/240 = 0,2(mol)
$C_2H_4 + Br_2 \to C_2H_4Br_2$
$C_2H_2 + 2Br_2 \to C_2H_2Br_4$
n Br2 = 2n C2H2 + n C2H4 = 80/160 = 0,5(mol)
=> n C2H4 = 0,5 - 0,2.2 = 0,1(mol)
Vậy :
%V C2H2 = 0,2.22,4/8,96 .100% = 50%
%V C2H4 = 0,1.22,4/8,96 .100% = 25%
%V CH4 = 100% -50% - 25% = 25%

\(n_{C_3H_3Ag}=\dfrac{7,35}{147}=0,05\left(mol\right)\)
=> \(n_{C_3H_4}=0,05\left(mol\right)\)
\(n_{Br_2}=\dfrac{6,4}{160}=0,04\left(mol\right)\)
=> \(n_{C_2H_4}=0,04\left(mol\right)\)
=> \(\left\{{}\begin{matrix}\%C_3H_4=\dfrac{0,05.40}{5,52}.100\%=36,23\%\\\%C_2H_4=\dfrac{0,04.28}{5,52}.100\%=20,29\%\\\%C_2H_6=100\%-36,23\%-20,29\%=43,48\%\end{matrix}\right.\)
=> A

Đáp án D
Đặt a, b, c lần lượt là số mol CH4, C2H4, C2H2 (trong 8,6 gam X)
Ta có: 16a + 28b + 26c = 8,6 (1)
b + 2c = 0,3 (2)
Mặt khác: Gọi số mol của CH4, C2H4, C2H2 trong 13,44 lít hỗn hợp X lần lượt là kx, ky, kz
![]() (3)
(3)
![]()
kc kc
Ta có
nkết tủa ![]() (4)
(4)
Lấy (3) chia (4) được
![]() (5)
(5)
Từ (1), (2) và (5) được

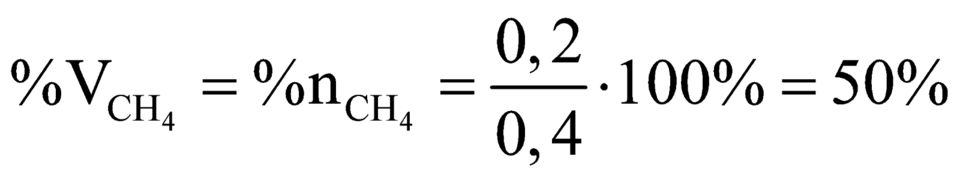

\(V_{C_2H_6}=13,44-6,72=6,72\left(l\right)\)
=> \(n_{C_2H_6}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\)
\(n_{C_2Ag_2}=\dfrac{24}{240}=0,1\left(mol\right)\)
=> \(n_{C_2H_2}=0,1\left(mol\right)\)
=> \(n_{C_2H_4}=\dfrac{13,44}{22,4}-0,3-0,1=0,2\left(mol\right)\)
=> \(\left\{{}\begin{matrix}\%m_{C_2H_6}=\dfrac{0,3.30}{0,3.30+0,2.28+0,1.26}.100\%=52,326\%\\\%m_{C_2H_4}=\dfrac{0,2.28}{0,3.30+0,2.28+0,1.26}.100\%=32,558\%\\\%m_{C_2H_2}=\dfrac{0,1.26}{0,3.30+0,2.28+0,1.26}.100\%=15,116\%\end{matrix}\right.\)