Cho 2 hàm số y= 2x + 6 (d)
y= -x+3 (d')
a, Vẽ đồ thị 2 hs trên cùng hệ trục tọa độ
b, Tìm tọa độ giao điểm A của 2 đg thẳng
c, Gọi B và C lần lượt là điểm của d va d' với trục Ox tính S tam giác ABC, C tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 12 2023
a: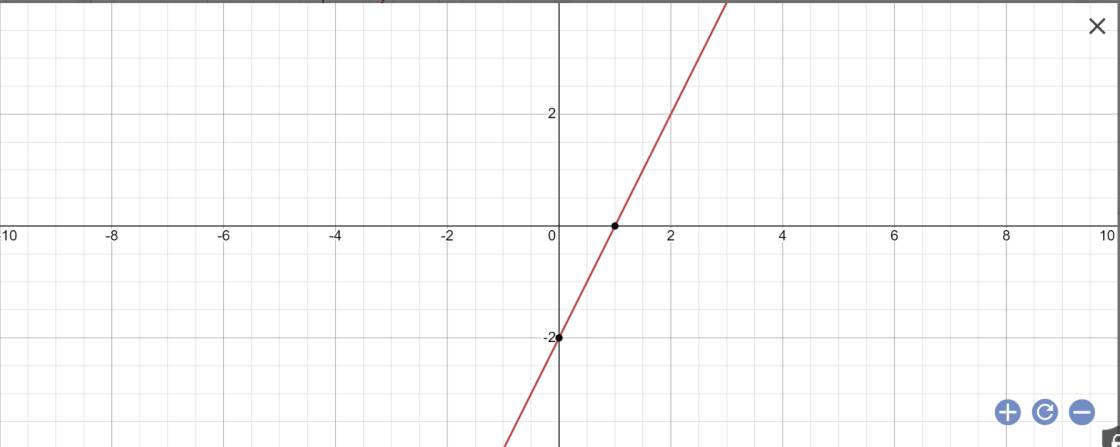 
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2022
\(y'=7\left(-x^2+3x+7\right)^6.\left(-x^2+3x+7\right)'\)
\(=7\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
25 tháng 10 2021
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
23 tháng 11 2021
\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)
CM
12 tháng 3 2019
a)
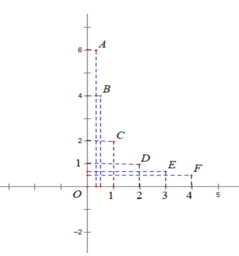
b)Bảng giá trị
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua 2 điểm (0; 0) và (1; 2)
22 tháng 12 2023
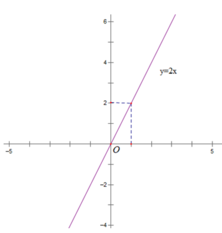
Bài 5:
a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)DB tại D
=>AD\(\perp\)BC tại D
Xét ΔABC vuông tại A có AD là đường cao
nên \(AC^2=CD\cdot CB\)
b: Ta có: ΔOAE cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOE
Xét ΔOAC và ΔOEC có
OA=OE
\(\widehat{AOC}=\widehat{EOC}\)
OC chung
Do đó: ΔOAC=ΔOEC
=>\(\widehat{OAC}=\widehat{OEC}\)
mà \(\widehat{OAC}=90^0\)
nên \(\widehat{OEC}=90^0\)
=>CE là tiếp tuyến của (O)
Bài 3:
a: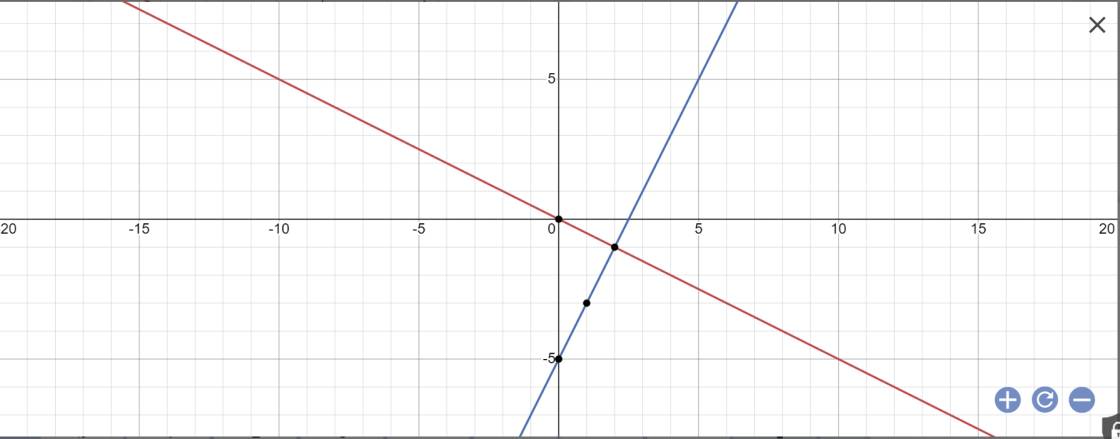 
b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x=2x-5\)
=>\(-\dfrac{1}{2}x-2x=-5\)
=>\(-\dfrac{5}{2}x=-5\)
=>x=2
Thay x=2 vào y=-1/2x, ta được:
\(y=-\dfrac{1}{2}\cdot2=-1\)
Vậy: (d) cắt (d') tại điểm A(2;-1)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 9 2021
a.
\(y'=-\dfrac{3}{2}x^3+\dfrac{6}{5}x^2-x+5\)
b.
\(y'=\dfrac{\left(x^2+4x+5\right)'}{2\sqrt{x^2+4x+5}}=\dfrac{2x+4}{2\sqrt{x^2+4x+5}}=\dfrac{x+2}{\sqrt{x^2+4x+5}}\)
c.
\(y=\left(3x-2\right)^{\dfrac{1}{3}}\Rightarrow y'=\dfrac{1}{3}\left(3x-2\right)^{-\dfrac{2}{3}}=\dfrac{1}{3\sqrt[3]{\left(3x-2\right)^2}}\)
d.
\(y'=2\sqrt{x+2}+\dfrac{2x-1}{2\sqrt{x+2}}=\dfrac{6x+7}{2\sqrt{x+2}}\)
e.
\(y'=3sin^2\left(\dfrac{\pi}{3}-5x\right).\left[sin\left(\dfrac{\pi}{3}-5x\right)\right]'=-15sin^2\left(\dfrac{\pi}{3}-5x\right).cos\left(\dfrac{\pi}{3}-5x\right)\)
g.
\(y'=4cot^3\left(\dfrac{\pi}{6}-3x\right)\left[cot\left(\dfrac{\pi}{3}-3x\right)\right]'=12cot^3\left(\dfrac{\pi}{6}-3x\right).\dfrac{1}{sin^2\left(\dfrac{\pi}{3}-3x\right)}\)
b) Phương trình hoành độ giao điểm là:
\(2x+6=-x+3\)
\(\Leftrightarrow2x+x=3-6\)
\(\Leftrightarrow3x=-3\)
hay x=-1
Thay x=-1 vào (d), ta được:
\(y=2\cdot\left(-1\right)+6=-2+6=4\)
Vậy: A(-1;4)