Bài 1: Cho hàm số y = (m-1)x + m, (với m là tham số) có đồ thị là đường thẳng (d)a) Xác định giá trị của m để đồ thị (d) của hàm số cắt trục tung tại điểm có tung độ bằng 2b) Xác định giá trị của m để đồ thị (d) của hàm số tạo với trục Ox 1 góc 45 độ. Khi đó hãy xác định công thức của đường thẳng (d') đi qua M(2;0) và song song với (d)Bài 2: Cho đường tròn tâm O dường kính...
Đọc tiếp
Bài 1: Cho hàm số y = (m-1)x + m, (với m là tham số) có đồ thị là đường thẳng (d)
a) Xác định giá trị của m để đồ thị (d) của hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Xác định giá trị của m để đồ thị (d) của hàm số tạo với trục Ox 1 góc 45 độ. Khi đó hãy xác định công thức của đường thẳng (d') đi qua M(2;0) và song song với (d)
Bài 2: Cho đường tròn tâm O dường kính BC, điểm A thuộc đường tròn. Vẽ bán kính OK song song với BA ( K và A nằm cùng phía đối diện với BC). Tiếp tuyến với đường tròn (O) tại C cắt OK ở I, OI cayws AC tại H. Chứng minh:
a) 4 điểm A, O, C, I cùng thuộc 1 đường tròn
b) IA là tiếp tuyến của đường tròn (O)
c) CK là phân giác của góc ACI
Bài 3: Cho tâm giác cân ABC (AB = AC), các đường cao AC, BE, CF cắt nhau tại H. Chứng mình:
a) 4 điểm A, E, H, F cùng thuộc 1 đường tròn tâm O đường kính AH
b) DE là tiếp tuyến của đường tròn (O)
c) DH.DA = DE.DE

Bài 5:
a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)DB tại D
=>AD\(\perp\)BC tại D
Xét ΔABC vuông tại A có AD là đường cao
nên \(AC^2=CD\cdot CB\)
b: Ta có: ΔOAE cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOE
Xét ΔOAC và ΔOEC có
OA=OE
\(\widehat{AOC}=\widehat{EOC}\)
OC chung
Do đó: ΔOAC=ΔOEC
=>\(\widehat{OAC}=\widehat{OEC}\)
mà \(\widehat{OAC}=90^0\)
nên \(\widehat{OEC}=90^0\)
=>CE là tiếp tuyến của (O)
Bài 3:
a: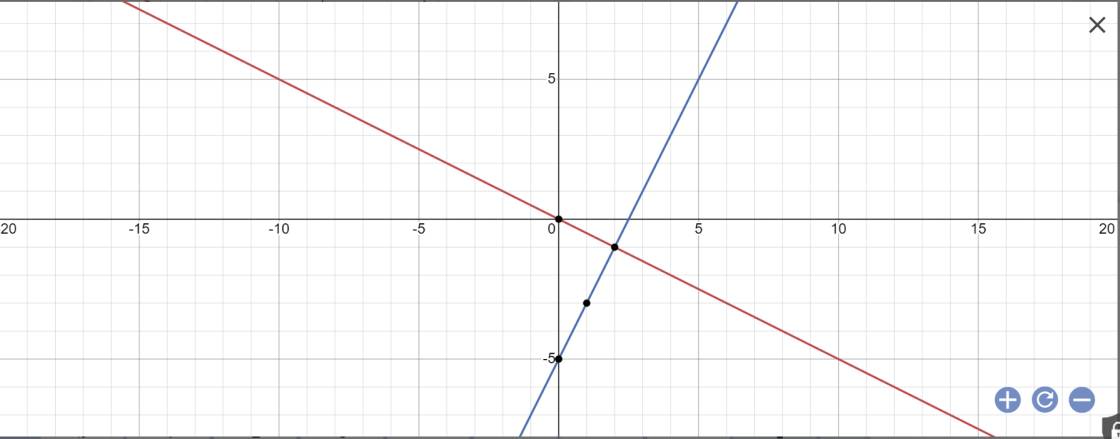
b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x=2x-5\)
=>\(-\dfrac{1}{2}x-2x=-5\)
=>\(-\dfrac{5}{2}x=-5\)
=>x=2
Thay x=2 vào y=-1/2x, ta được:
\(y=-\dfrac{1}{2}\cdot2=-1\)
Vậy: (d) cắt (d') tại điểm A(2;-1)