Cho 2 nguồn sóng kết hợp \(P_1,P_2\) cách nhau 32cm. Sóng do hai nguồn phát ra có bước sóng \(\lambda=10cm\) và có biểu thức lần lượt là \(u_1=a\cos\left(2\pi ft\right)\)và \(u_2=a\cos\left(2\pi ft+\frac{\pi}{2}\right)\). Tính số vân dao động với biên độ cực đại, cực tiểu trong đoạn \(P_1P_2\)?
A.7 vân cực đại, 6 vân cực tiểu.
B.6 vân cực đại, 6 vân cực tiểu.
C.6 vân cực đại, 7 vân cực tiểu.
D.7 vân cực đại, 7 vân cực tiểu.

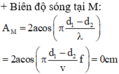

\(\triangle \varphi = \frac{\pi}{2}.\)
Số điểm dao động vân cực đại trên đoạn thẳng nối hai nguồn là:
\(-AB\leq d_2-d_1\leq AB \Rightarrow -AB\leq (k+\frac{\triangle\varphi)}{2 \pi}\lambda\leq AB \\ \Rightarrow -32 \leq (k+ \frac{1}{4}) \lambda \leq 32 \Rightarrow -3,45 \leq k \leq 2,95 \\ \Rightarrow k = -3,-2,-1,0,1,2.\)
Có 6 vân cực đại.
Số điểm dao động vân cực tiểu trên đoạn thẳng nối hai nguồn là:
\(-AB\leq d_2-d_1\leq AB \Rightarrow -AB\leq (2k+1+\frac{\triangle\varphi}{\pi})\frac{\lambda}{2}\leq AB \\ \Rightarrow -32 \leq (2k+1+\frac{1}{2})5 \leq 32 \\ \Rightarrow -3,95 \leq k \leq 2,45. \\ \Rightarrow k = -3,-2,-1,0,1,2.\)
Có 6 vân cực tiểu.
B