Một vật tgia đồg thời 2dđ cùg phương cùng f và lệch pha nhau 1góc pi/2 .nếu tgia dđ 1 cơ năng là W1 .nếu chỉ tgia dđ 2 thì W là W2 + 3W1 .khi tgia hai dđ thì W = ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
30 tháng 4 2016
Bước sóng \(\lambda=v.T=2.20=40cm\)
M cùng pha với O, thì M cách O nguyên lần bước sóng \(\Rightarrow MO = k\lambda=40.k(cm)\)
N gần nhất vuông pha với M thì \(MN=\dfrac{\lambda}{4}=10(cm)\)
Suy ra: \(NO=MO\pm MN = 40k\pm 10(cm)\)
30 tháng 12 2015
\(T=2\pi\sqrt{\dfrac{m}{k}}\)
\(\Rightarrow \dfrac{T_2}{T_1}=\sqrt{\dfrac{m_2}{m_1}}=2\)
\(\Rightarrow\dfrac{m_2}{m_1}=4\)(1)
Nếu treo cả hệ hai vật vào lò xo thì \(T'=2\pi\sqrt{\dfrac{m_1+m_2}{k}}=\dfrac{\pi}{5}\)
\(\Rightarrow m_1+m_2=1kg\) (2)
Từ (1) và (2) suy ra: \(m_1=0,2kg, m2=0,4kg\)
Like cho tớ để động viên tinh thần nhá 
VT
14 tháng 10 2018
Đáp án D
Bia dao động điều hòa mà để xác suất trúng cao nhất thì bia di chuyển chậm nhất → trong quá trình dao động, tốc độ nhỏ nhất tại biên → để số lần trúng nhiều nhất thì nên chĩa súng vào vùng 1 hoặc 5
NH
3 tháng 7 2016
f = 20 Hz \(\Rightarrow\) \(\omega\) = 2\(\pi\). f = 2\(\sqrt{10}\). 20 = 40\(\pi\) (rad/s)
x= 2\(\sqrt{3}\) ; A = 4cm
Lúc t=0 (s)
\(\left[\begin{array}{nghiempt}x=2\sqrt{3}\left(1\right)\\v< 0\left(2\right)\end{array}\right.\)
Giải (1) : cosφ = \(\frac{2\sqrt{3}}{4}\)= \(\frac{\sqrt{3}}{2}\)
\(\Rightarrow\) φ = \(\pm\) \(\frac{\pi}{6}\)
Giải (2) : v < 0 \(\Rightarrow\sin\varphi\) >0
Suy ra φ = \(\frac{\pi}{6}\)
PT dao động: \(x=4\cos\left(40\pi t+\frac{\pi}{6}\right)\) (cm)
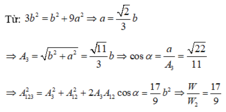
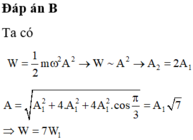
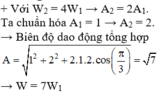
Do hai dao động thành phần vuông pha nhau, nên biên độ dao động tổng hợp: \(A^2=A_1^2+A_2^2\)
Cơ năng: \(W=\dfrac{1}{2}kA^2=\dfrac{1}{2}k(A_1^2+A_2^2)=\dfrac{1}{2}kA_1^2+\dfrac{1}{2}kA_2^2\)\(=W_1+(W_2+3W_1)=W_2+4W_1\)