đặt điện áp xoay chiều u=Uocos(100pit + phi) vào hai đầu đoạn mạch gồm R,L,C mắc nối tiếp
C=10^-4/pi R không đổi, L thay đổi được.
Khi L=2/pi thì biểu thức cường độ dòng điện i=I1căn2cos(100pit-pi/12)
L=4/pi thì biểu thức của dòng điện i=I2căn2cos(100pit-pi/4)
giá trị điện trở R gần với giá trị nào nhất
A.145 B.170 C.247 D.238

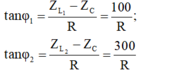
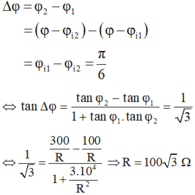
\(Z_C=100\Omega\)
\(Z_{L1}=200\Omega\)
\(Z_{L2}=400\Omega\)
Ta biểu diễn trên giản đồ véc tơ sự thay đổi của L như sau:
R Zc ZL2 ZL1 Z1 Z2 30 100 100 200 x O
Ta có: \(\tan30=\tan\left(Z_2OR-Z_1OR\right)=\frac{\tan Z_2OR-\tan Z_1OR}{1+\tan Z_2OR.\tan Z_1OR}\)
Suy ra: \(\frac{1}{\sqrt{3}}=\frac{\frac{300}{x}-\frac{100}{x}}{1+\frac{300}{x}.\frac{100}{x}}\)
Giải pt này em sẽ tìm đc x.