1. Một sóng cơ học có bước sóng truyền từ A đến M (AM=d) . M dao động ngược pha với A khi ?
2.Một sóng truyền theo trục Ox được mô tả bởi phương trình u=8sin2pi ( 0,5pi.x-4pi.t) (cm ) trong đó x tính bằng mét , t tính bằng giây . Vận tốc truyền sóng là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 9 2015
Đề nghị bạn gửi mỗi bài một câu thôi, nhìn thế này hoa mắt quá :)
1. Chu kì sóng: \(T=\frac{2\pi}{\omega}=\frac{2\pi}{4\pi}=0,5s\)
Bước sóng: \(\lambda=v.T=12.0,5=6m\)
Độ lệch pha giữa 2 điểm: \(\Delta\varphi=\frac{2\pi d}{\lambda}=\frac{2\pi.1,5}{6}=\frac{\pi}{2}\)
VT
23 tháng 1 2018
Đáp án B
+ Độ lệch pha giữa hai điểm A và B:
∆ φ A B = 2 π ∆ x A B f v = ( 2 k + 1 ) π → v = 4 2 k + 1 m/s
+ Với khoảng giả trị của vận tốc: 0 , 7 m / s ≤ v ≤ 1 m / s → v = 0 , 8 m → λ = 4 cm
VT
9 tháng 3 2019
Đáp án: B
HD Giải: Tốc độ truyền sóng v = H e _ s o _ t r u o c _ t H e _ s o _ t r u o c _ x = 1000 50 = 20 c m / s
Tốc độ cực đại của phần tử v m a x = ω A = 1000.0,5 = 500 cm/s = 25v
VT
17 tháng 2 2018
Đáp án D
Phương pháp: Viết phương trình dao động của phần tử môi trường tại M và xét đặc điểm của nó
Cách giải:
Phương trình dao động của nguồn O là:
Phương trình dao động của phần tử bất kì là:
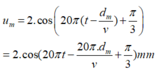
Biết d m < 42,5 cm. và vận tốc v = 1m/s = 100cm/s.
Phần tử m dao động lệch pha π/6 so với nguồn tức là:
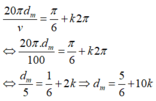
Áp dụng điều kiện 0 < d m < 42,5 cm ta có :
VT
24 tháng 6 2019
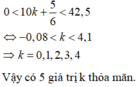
Đáp án D
Phương pháp: Viết phương trình dao động của phần tử môi trường tại M và xét đặc điểm của nó
Cách giải:
Phương trình dao động của nguồn O là: u 0 = 2 cos ( 20 π t + π 3 ) m m
Phương trình dao động của phần tử bất kì là:
u m = 2 cos ( 20 π ( t - d m v ) + π 3 ) = 2 cos ( 20 π t - 20 π d m v + π 3 ) mm
Biết dm < 42,5 cm. và vận tốc v = 1m/s = 100cm/s.
Phần tử m dao động lệch pha π/6 so với nguồn tức là:
20 π d m v = π 6 + k 2 π ⇔ 20 π . d m 100 = π 6 + k 2 π ⇔ d m 5 = 1 6 + 2 k ⇔ d m = 5 6 + ' 10 k
Áp dụng điều kiện 0 < dm < 42,5 cm ta có : 0 < 10 k + 5 6 < 42 , 5 ⇔ - 0 , 08 < k < 4 , 1 ⇒ k = 0 , 1 , 2 , 3 , 4
Vậy có 5 giá trị k thỏa mãn.
1. Độ lệch pha giữa A và M: \(\Delta\varphi=\frac{2\pi d}{\lambda}\)
M ngược pha với A khi: \(\Delta\varphi=\left(2k+1\right)\pi\Leftrightarrow\frac{2\pi d}{\lambda}=\left(2k+1\right)\pi\Leftrightarrow d=\left(k+0,5\right)\lambda\)
2. \(u=8\sin\left(\pi^2x-8\pi^2t\right)\)
Suy ra: \(\begin{cases}T=\frac{2\pi}{8\pi^2}=\frac{1}{4\pi}\\\pi^2x=\frac{2\pi x}{\lambda}\end{cases}\Leftrightarrow\begin{cases}T=\frac{1}{4\pi}\\\lambda=\frac{2}{\pi}\end{cases}\)
Vậy \(v=\frac{\lambda}{T}=8\)(m/s)