Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tự kẻ hình nha
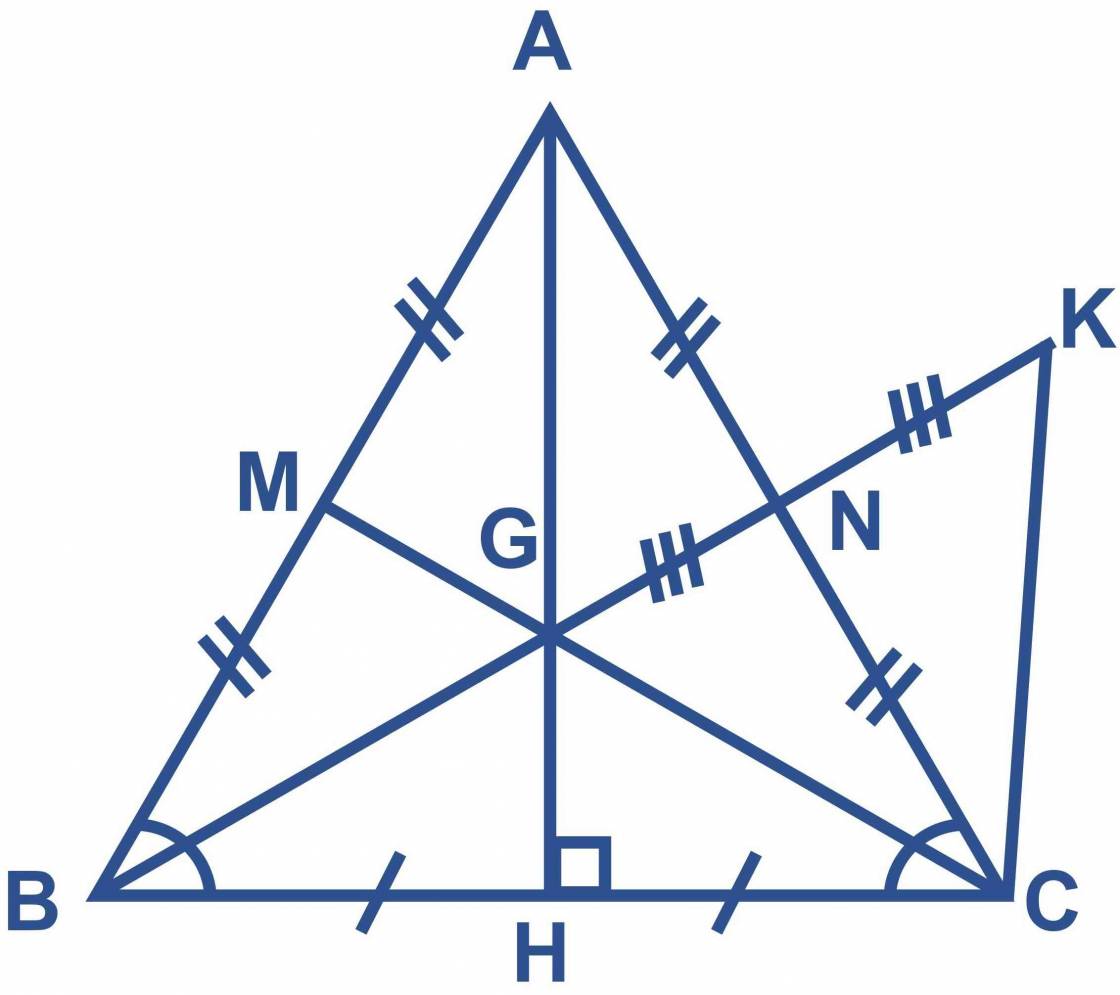
a) - Vì tam giác ABC cân tại A (gt)
=> AB = AC (định nghĩa)
góc ABC = góc ACB (dấu hiệu)
- Vì AH vuông góc với BC (gt)
=> tam giác ABH vuông tại H (tc)
tam giác ACH vuông tại H (tc)
- Xét tam giác vuông ABH và tam giác vuông ACH, có:
+ AB = AC (cmt)
+ Chung AC
=> tam giác vuông ABH = tam giác vuông ACH (cạnh huyền - cạnh góc vuông)
b) - Vì tam giác vuông ABH = tam giác vuông ACH (cmt)
=> BH = CH (2 cạnh tương ứng)
=> AH là đường trung tuyến tam giác ABC (dấu hiệu)
- Vì N là trung điểm của AC (gt)
=> BN là đường trung tuyến tam giác ABC (dấu hiệu)
Mà G là giao điểm của BN và AH (gt)
=> G là trọng tâm của tam giác ABC (tc)
- Xét tam giác ANG và tam giác CNK, có:
+ NG = NK (gt)
+ AN = CN (N là trung điểm của AC)
+ góc ANG = góc CNG (đối đỉnh)
=> tam giác ANG và tam giác CNK (cgc)
=> góc AGN = góc CKN (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=> AG // CK (dấu hiệu)
c) - Vì G là trọng tâm của tam giác ABC (cmt)
=> BG = 2/3 BN (tc)
=> NG = 1/3 BN
Mà NK = NG (gt)
=> NK = 1/3 BN
=> NK + NG = 1/3 BN + 1/3 BN
=> GK = 2/3 BN
Mà BG = 2/3 BN (cmt)
=> GK = BG
=> G là trung điểm BK
a)xét 2 tam giác vuông ABH và tam giác ACH có:
AB=AC(GT)
góc ABH=góc ACH(GT)
\(\Rightarrow\) tam giácABH = tam giác ACH(cạnh huyền-góc nhọn)
b)xét 2 tam giác ANG và tam giác CNK có:
CN=AN(GT)
góc KNC=góc ANG(2 góc đối đỉnh)
GN=KN(GT)
\(\Rightarrow\)tam giác ANG=tam giác CNK(c-g-c)
\(\Rightarrow\)Góc GAN=góc KCN
Vì góc GAN=góc KCN,mà 2 góc này ở vị trí so le trong
\(\Rightarrow\)AH//CK
a) trong ΔABC, có góc AHB là góc vuông
góc ABH là góc nhọn
⇒ góc AHB > góc ABH
⇒ AB > AH
b) M là trung điểm của AB và N là trung điểm của AC, mà AB = AC (2 cạnh bên của tam giác cân) ⇒ MB = NC
xét tam giác MBC và tam giác NCB, ta có :
MB = NC (cmt)
góc B = góc C (2 góc đáy của 1 tam giác cân)
BC là cạnh chung
⇒ tam giác MBC = tam giác NCB (c-g-c)
⇒ MC = NB (2 cạnh tương ứng)
c) xét tam giác NAG và tam giác NCK , ta có :
NA = NC (vì N là trung điểm của cạnh AC)
góc NAG = góc NCK (đối đỉnh)
NG = NK (gt)
=> tam giác NAG = tam giác NCK (c-g-c)
=> AG = CK (2 cạnh tương ứng)
a, Xét tg AHB và tg AHC, có:
AB=AC(tg cân)
góc AHB= góc AHC(=90o)
AH chung.
=>tg AHB= tg AHC( ch-cgv)
=>BH=HC.
=>H là trung điểm của BC.
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
b: Sửa đề: Trên tia đối của tia HA
Xét ΔABH vuông tại H và ΔDCH vuông tại H có
HA=HD
HB=HC
Do đó: ΔABH=ΔDCH
c: Sửa đề: Cm ΔACD cân
Ta có: ΔABH=ΔDCH
=>DC=AB
mà AB=AC
nên CA=CD
=>ΔCAD cân tại C
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔAHC
Suy ra: BH=CH
hay H là trung điểm của BC
b: Xét ΔABH vuông tại H và ΔDCH vuông tại H có
HB=HC
HA=HD
Do đó: ΔABH=ΔDCH
c: Ta có: ΔABH=ΔDCH
nên AB=DC
mà AB=AC
nên DC=AC
hay ΔACD cân tại C
a, △ABH=△ACH (ch-cgv) (tự cm)
hoặc △ABH=△ACH (ch-gn) (tự cm)
b, Xét \(\Delta ANG\) và \(\Delta CNK\) có:
AN = CN ( vì N là tđ của AC)
ANG = CNK ( vì đđ)
GN = KN (gt)
=> \(\Delta ANG=\Delta CNK\) (c-g-c).
=> GAN = KCN (hai góc t/ứng).
Mà GAN và KCN ở vị trí slt nên:
=> AG//CK (đpcm).
c, Do tam giác ABC có: N là tđ của AC nên:
=> BN là đg trung tuyến của AC cắt AH tại G (1)
Do tam giác ABC có: AH vừa là đg cao nên:
=> AH cũng là đg trung tuyến của BC (t/ch trong tam giác cân) (2)
Xét \(\Delta ABC\) có: Từ (1) và (2) => G là trọng tâm của \(\Delta ABC\)
=> \(BG=2GN\) (3)
Ta có: GN + NK = GK
hay GN + GN = GK
=> GK = 2GN (4)
Từ (3) và (4) => BG = GK
=> G là tđ của BK (đpcm)
Câu d có vấn đề nhờ bạn xem lại cho mk cái!
Chúc bạn học tốt! Nhớ theo dõi cho mk vs ạ.
ghhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
mấy bạn bớt nhắn linh tinh lên đây đi, olm là nơi học bài và hỏi bài chứ không phải nhắn lung tung
a, △ABH=△ACH (ch-cgv) (tự cm)
hoặc △ABH=△ACH (ch-gn) (tự cm)
b, Xét ΔANGΔANG và ΔCNKΔCNK có:
AN = CN ( vì N là tđ của AC)
ANG = CNK ( vì đđ)
GN = KN (gt)
=> ΔANG=ΔCNKΔANG=ΔCNK (c-g-c).
=> GAN = KCN (hai góc t/ứng).
Mà GAN và KCN ở vị trí slt nên:
=> AG//CK (đpcm).
c, Do tam giác ABC có: N là tđ của AC nên:
=> BN là đg trung tuyến của AC cắt AH tại G (1)
Do tam giác ABC có: AH vừa là đg cao nên:
=> AH cũng là đg trung tuyến của BC (t/ch trong tam giác cân) (2)
Xét ΔABCΔABC có: Từ (1) và (2) => G là trọng tâm của ΔABCΔABC
=> BG=2GNBG=2GN (3)
Ta có: GN + NK = GK
hay GN + GN = GK
=> GK = 2GN (4)
Từ (3) và (4) => BG = GK
=> G là tđ của BK (đpcm)
a, △ABH=△ACH (ch-cgv) (tự cm)
b, Xét ΔANG và ΔCNK có:
AN = CN ( vì N là tđ của AC)
ANG = CNK ( vì đđ)
GN = KN (gt)
=> ΔANG=ΔCNKΔANG=ΔCNK (c-g-c).
=> GAN = KCN (hai góc t/ứng).
Mà GAN và KCN ở vị trí slt nên:
=> AG//CK (đpcm).
c, Do tam giác ABC có: N là tđ của AC nên:
=> BN là đg trung tuyến của AC cắt AH tại G (1)
Do tam giác ABC có: AH vừa là đg cao nên:
=> AH cũng là đg trung tuyến của BC (t/ch trong tam giác cân) (2)
Xét ΔABCΔABC có: Từ (1) và (2) => G là trọng tâm của ΔABCΔABC
=> BG=2GNBG=2GN (3)
Ta có: GN + NK = GK
hay GN + GN = GK
=> GK = 2GN (4)
Từ (3) và (4) => BG = GK
=> G là tđ của BK (đpcm)