tìm tìm x,y,z, thoả mãn x^2+y^2+z^2=4x-2y+6=-14
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TP
1
B
19 tháng 9 2015
bạn sẽ có: 2x^2/(1-x^2) - y = 0 => -2x^2/(x^2 -1) = y => 2x^2/(x^2 - 1) = - y. hay 2 + 2/(x^2 - 1) = -y(1). chứng minh tương tự bạn sẽ có 2y^2/(1-y^2)-z = 0 + => 2 + 2/(y^2-1) = -z(2) và 2z^2/(1-z^2) - x = 0 => 2 + 2/(z^2 -1) = - x(3).bạn đặt x^2 - 1 = a. y^2 - 1 = b. z^2 - 1 = c. => thế vào (1) (2) (3) bạn sẽ có:
2 + 2/b = -căn(c + 1)
2 + 2/a = - căn(b + 1)
2 + 2/c = - căn(a +1)
đặt căn (c+1) = m. căn (b +1) = n. căn (a + 1) = p thay vào hpt sẽ có:
2 + 2/b = -m
2 + 2/a = -n
2 +2/c = -p
giải hệ phương trình này ra bạn sẽ ra được a, b , c và từ đó bạn sẽ tìm ra được x ,y,z còn lại bạn tự làm nốt nhé. Tớ lười tính quá :|
VN
Võ Ngọc Phương
VIP
27 tháng 12 2023
Ta có: \(4x=3y\) hay \(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{9}=\dfrac{y}{12}\left(1\right)\)
\(4y=3z\) hay \(\dfrac{y}{3}=\dfrac{z}{4}\Rightarrow\dfrac{y}{12}=\dfrac{z}{16}\left(2\right)\)
Từ (1) và (2), suy ra:
\(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{16}\) \(\Rightarrow\dfrac{2x}{18}=\dfrac{y}{12}=\dfrac{z}{16}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{2x}{18}=\dfrac{y}{12}=\dfrac{z}{16}=\dfrac{2x+y-z}{18+12-16}=\dfrac{-14}{14}=-1\)
Do đó:
\(\dfrac{x}{9}=-1\Rightarrow x=9.\left(-1\right)=-9\)
\(\dfrac{y}{12}=-1\Rightarrow y=12.\left(-1\right)=-12\)
\(\dfrac{z}{16}=-1\Rightarrow z=16.\left(-1\right)=-16\)
Vậy x = -9 ; y = -12 ; z = -16
DP
1
18 tháng 4 2023
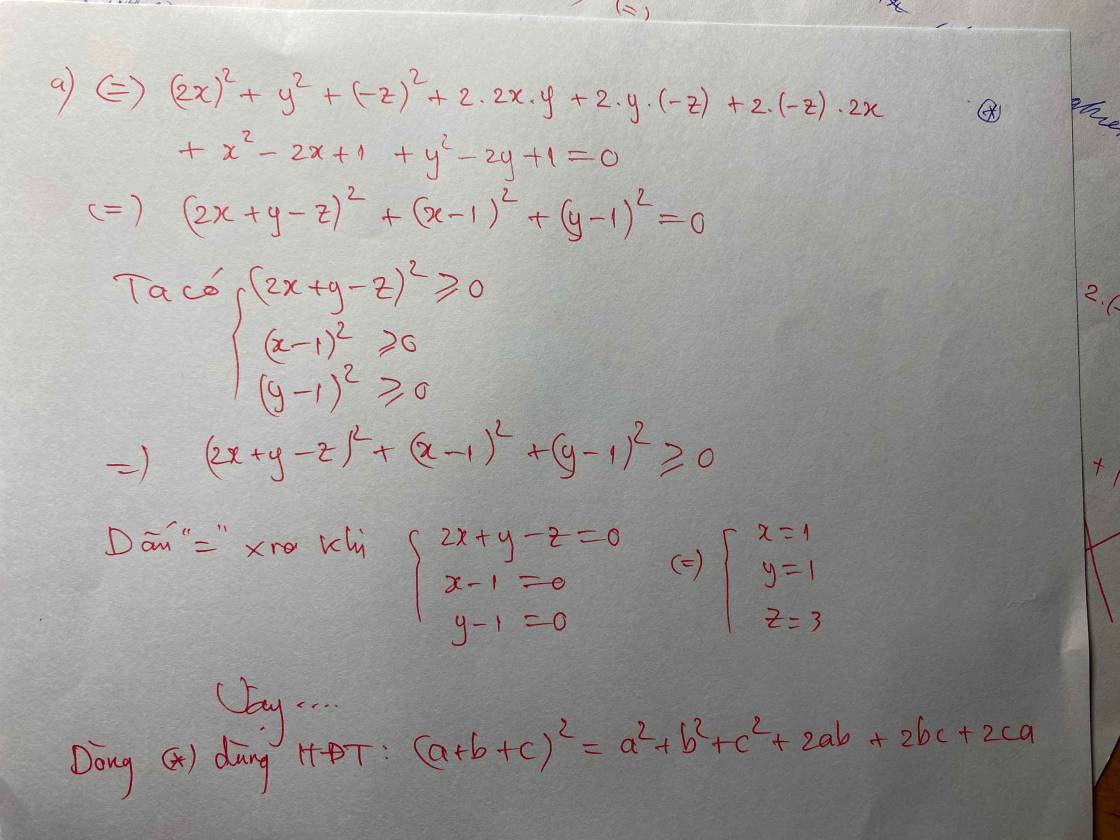
Học tốt nha bn ! ( dòng * ko cần ghi vào đâu bn đây là nháp giở của mik )
MT
1
2 tháng 10 2021
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y+1}{3}=\dfrac{z}{5}=\dfrac{x-1+2y+2-2z}{2+6-10}=\dfrac{-3}{-2}=\dfrac{3}{2}\)
Do đó: \(\left\{{}\begin{matrix}x-1=3\\y+1=\dfrac{9}{2}\\z=5\cdot\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=\dfrac{7}{2}\\z=\dfrac{15}{2}\end{matrix}\right.\)
AN
1
DD
Đoàn Đức Hà
Giáo viên
6 tháng 7 2021
\(x^2-2xy+2y^2+5z^2+4yz-4z+4=0\)
\(\Leftrightarrow x^2-2xy+y^2+y^2+4yz+4z^2+z^2-4z+4=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y+2z\right)^2+\left(z-2\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x-y=0\\y+2z=0\\z-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-4\\y=-4\\z=2\end{cases}}\)
13 tháng 10 2019
\(x^2+y^2+z^2=4x-2y+6z-14\)
\(\Leftrightarrow x^2-4x+4+y^2+2y+1+z^2-6z+9=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y+1\right)^2+\left(z-3\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}x-2=0\\y+1=0\\z-3=0\end{cases}\Rightarrow\hept{\begin{cases}x=2\\y=-1\\z=3\end{cases}}}\)
13 tháng 10 2019
\(\Leftrightarrow\) \(x^2\)+ \(y^2\) + \(z^2\) - \(4x\)+ \(2y\) - \(6z\) + \(14\) \(=\) \(0\)
\(\Leftrightarrow\) ( \(x^2\) - \(4x\) + \(4\) ) + ( \(y^2\) + \(2y\) + \(1\) ) \(=\) \(0\)
\(\Leftrightarrow\) ( \(x-2\))2 + \(\left(y+1\right)^2\) + \(\left(z-3\right)^2\) \(=\) \(0\)
\(\Leftrightarrow\) \(\hept{\begin{cases}x=2\\y=-1\\z=3\end{cases}}\)
Ta thấy $x^2+y^2+z^2\geq 0$ với mọi $x,y,z$
Do đó $x^2+y^2+z^2=-14$ là vô lý
PT vô nghiệm.
\(x^2+y^2+z^2=4x-2y+6=-14\)
⇔ \(x^2-4x+4+y^2+2y+1+z^2-6z+9=0\)
⇔ \(\left(x-2\right)^2+\left(y+1\right)^2+\left(z-3\right)^2=0\)
⇔ \(\left\{{}\begin{matrix}\left(x-2\right)^2\\\left(y+1\right)^2\\\left(z-3\right)^2\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x=2\\y=-1\\z=3\end{matrix}\right.\)