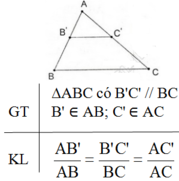
Chứng minh định lí Talet thuận.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Cho tgiac ABC với MN//BC, M,N thuộc AB,AC
Kẻ \(BH\perp AC\), ta có: \(\frac{S_{ANB}}{S_{ABC}}=\frac{\frac{1}{2}BH.AN}{\frac{1}{2}BH.AC}=\frac{AN}{AC}\left(1\right)\)
Tương tự ta cũng có: \(\frac{S_{AMC}}{S_{ABC}}=\frac{AM}{AB}\left(2\right)\)
Ta cần CM (1)=(2)
Ta có: \(S_{ANB}=S_{AMN}+S_{MNB}\left(3\right)\)
\(S_{AMC}=S_{AMN}+S_{MNC}\left(4\right)\)
Mà MN//BC nên : \(S_{MNB}=S_{MNC}\Rightarrow\left(3\right)=\left(4\right)\)
Từ đó có: \(S_{ANB}=S_{AMC}\Rightarrow\left(1\right)=\left(2\right)\Rightarrow\frac{AN}{AC}=\frac{AM}{AB}\)
A B C M N

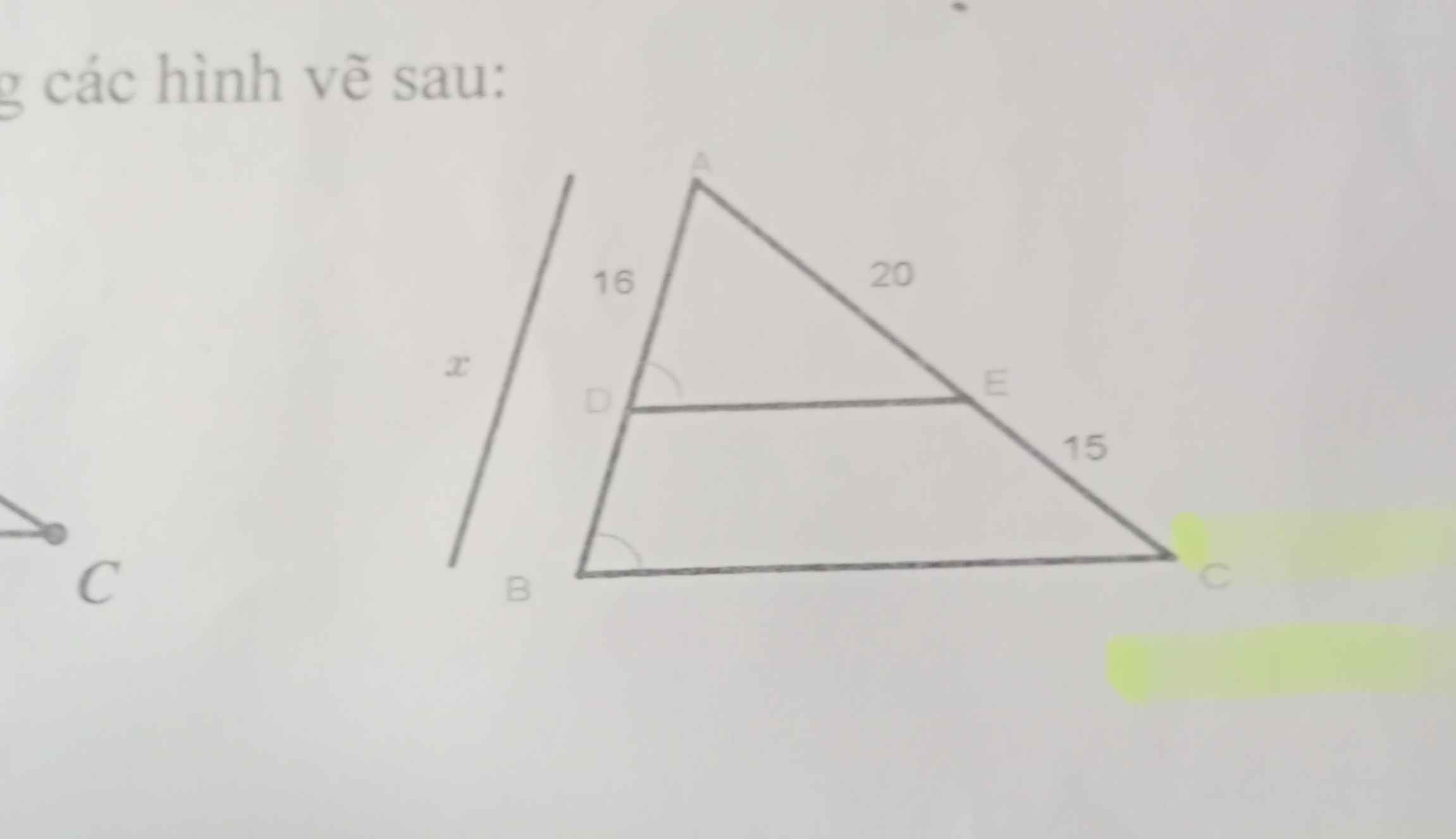
Áp dụng đl ta-lét vào tam giác ABC có DE//BC có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay \(\dfrac{16}{DB}=\dfrac{20}{15}\Rightarrow DB=16:\dfrac{20}{15}=12\)
\(\Rightarrow x=AD+DB=16+12=28\)

Định lí Talet đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
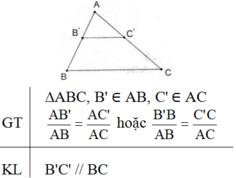

Câu 1:
*Định lí Ta - lét thuận: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
*Định lí Ta - lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Câu 2:
*Định lí Ta - lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
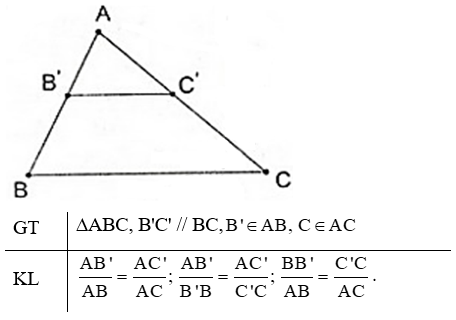
Hệ quả của định lí Talet
Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.


Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
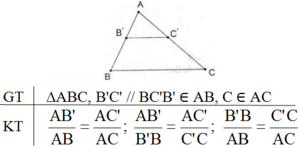

Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.