Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



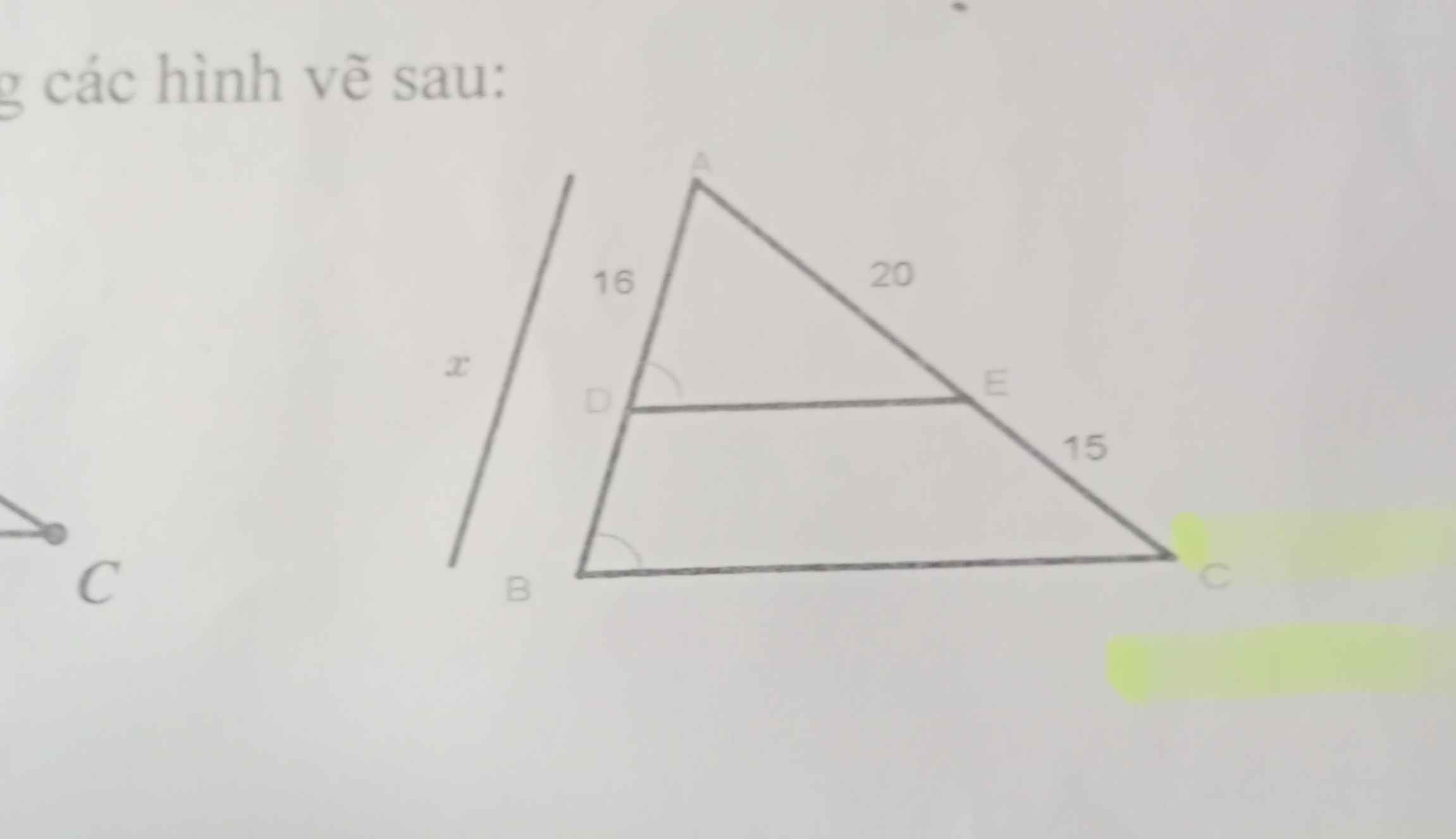
Áp dụng đl ta-lét vào tam giác ABC có DE//BC có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay \(\dfrac{16}{DB}=\dfrac{20}{15}\Rightarrow DB=16:\dfrac{20}{15}=12\)
\(\Rightarrow x=AD+DB=16+12=28\)

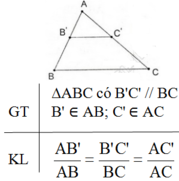
Định lí Talet đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
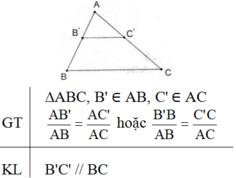

Định lí Talet trong tam giác:
Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
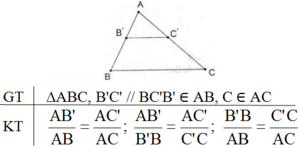

Hệ quả của định lí Talet:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.

Định lí CEVA
Cho tam giác ABC với các điểm M, N, P khác A, B, C theo thứ tự thuộc BC, CA, AB. Khi đó các đường thẳng AM, BN. CP đồng quy hoặc đôi một song song khi chỉ khi \(\frac{\overline{MB}}{\overline{MC}}.\frac{\overline{NC}}{\overline{NA}}.\frac{\overline{PA}}{\overline{PB}}=-1\)
Bài làm:
Y X A B C P O N M
ĐIỀU KIỆN CẦN
Trường hợp 1: AM, BN, CP đồng quy
Giả sử AM, BN, CP đồng quy tại O. Qua A vẽ đường thẳng song song với BC đường thẳng này cắt BN, CP lần lượt tại X, Y
Áp dụng Talet ta có:
\(\frac{\overline{MB}}{\overline{MC}}.\frac{\overline{NC}}{\overline{NA}}.\frac{\overline{PA}}{\overline{PB}}=\frac{\overline{AX}}{\overline{AY}}.\frac{\overline{BC}}{\overline{XA}}.\frac{\overline{YA}}{\overline{CB}}=\frac{\overline{AX}}{\overline{XA}}.\frac{\overline{BC}}{\overline{CB}}.\frac{\overline{YA}}{\overline{AY}}=\left(-1\right).\left(-1\right).\left(-1\right)=-1\)
Trường hợp 2: AM, BN, CP đôi một song song
A B C N M P
Áp dụng TALET ta có:
\(\frac{\overline{MB}}{\overline{MC}}.\frac{\overline{NC}}{\overline{NA}}.\frac{\overline{PA}}{\overline{PB}}=\frac{\overline{MB}}{\overline{MC}}.\frac{\overline{BC}}{\overline{BM}}.\frac{\overline{CM}}{\overline{CB}}=\frac{\overline{MB}}{\overline{BM}}.\frac{\overline{BC}}{\overline{CB}}.\frac{\overline{CM}}{\overline{MC}}=\left(-1\right).\left(-1\right).\left(-1\right)=-1\)
Như vậy trong cả 2 trường hợp ta đều có: \(\frac{\overline{MB}}{\overline{MC}}.\frac{\overline{NC}}{\overline{NA}}.\frac{\overline{PA}}{\overline{PB}}=-1\)
p/s: điều kiện đủ và MELELAUS tối mai c/m tiếp, bh mk bận
ĐIỀU KIỆN ĐỦ: Ta chứng minh nếu 3 đường AM, BN, CP không đôi một song song thì chúng đồng quy
A B C N O M
Giả sử AM, BN không song song. Đặt O là giao điểm của AM và BN
Khi đó CO và AB không song song. Thật vậy nếu CO và AB song song thì theo Talet ta có:
\(\frac{\overline{MB}}{\overline{MC}}=\frac{\overline{AB}}{\overline{OC}}=-\frac{\overline{AB}}{\overline{CA}}=-\frac{\overline{NA}}{\overline{NC}}\Rightarrow\frac{\overline{MB}}{\overline{,MC}}.\frac{\overline{NC}}{\overline{NA}}=-1\)
Mặt khác theo giải thiết: \(\frac{\overline{MB}}{\overline{MC}}.\frac{\overline{NC}}{\overline{NA}}.\frac{\overline{PA}}{\overline{PB}}=-1\)
suy ra: \(\frac{\overline{PA}}{\overline{PB}}=1\)\(\Rightarrow\)\(\overline{PA}=\overline{PB}\)\(\Rightarrow\)\(A\equiv B\)mâu thuẫn
Vậy CO không song song với AB.
Đặt P' là giao của CO với AB
Theo kết quả đạt được trong c/m đk cần \(\frac{\overline{MB}}{\overline{MC}}.\frac{\overline{NC}}{\overline{NA}}.\frac{\overline{P'A}}{\overline{P'B}}=-1\)
Từ đó với: \(\frac{\overline{MB}}{\overline{MC}}.\frac{\overline{NC}}{NA}.\frac{\overline{PA}}{\overline{PB}}=-1\)
ta có: \(\frac{\overline{P'A}}{\overline{P'B}}=\frac{\overline{PA}}{\overline{PB}}\) \(\Rightarrow\)\(P'\equiv P\)
Như vậy AM, BN, CP đồng quy

Sao cậu không tra trên google
Các cách chứng minh định lý pytago là :
Link :
www.bachkhoatrithuc.vn - Các cách chứng minh định lý Pitago,
Định lý có thể chứng minh bằng phương pháp đại số khi sử dụng 4 tam giác vuông bằng nhau có các cạnh a, b và c, các tam giác này được sắp xếp thành một hình vuông lớn có cạnh là cạnh huyền c. Các tam giác bằng nhau có diện tích , khi đó hình vuông nhỏ bên trong có cạnh là b − a và diện tích là (b − a)2.

n = 3 đúng.
Với n >=4. Từ 1 đỉnh của đa giác ta nối được với n - 2 đỉnh ( trừ 2 đỉnh liền kề ) ta được n-2 tam giác => dpcm.
Từ bài này ta đi đến cm được tổng các góc ngoài của 1 đa giác luôn bằng 360o.