Cho A là tổng lập phương các số tự nhiên từ 1 đến n và B là bình phương tổng các số tự nhiên từ 1 đến n. Người ta đã chứng minh được rằng A=B. Bạn hãy chứng minh điều đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 2 2021
Với n=4 thì
\(A=1^3+2^3+3^3+4^3=1+8+27+64=100\)
\(B=\left(1+2+3+4\right)^2=10^2=100\)
nên A=B
Với n=5 thì
\(A=1^3+2^3+3^3+4^3+5^3=1+8+27+64+125=225\)
\(B=\left(1+2+3+4+5\right)^2=15^2=225\)
nên A=B
Với n=6 thì
\(A=1^3+2^3+3^3+4^3+5^3+6^3=1+8+27+64+125+216=441\)
\(B=\left(1+2+3+4+5+6\right)^2=21^2=441\)
nên A=B
22 tháng 6 2022
n=4 thì \(A=1^3+2^3+3^3+4^3=100\)
\(B=\left(1+2+3+4\right)^2=10^2=100\)
Do đó: A=B
n=5 thì \(A=1^3+2^3+3^3+4^3+5^3=225\)
\(B=\left(1+2+3+4+5\right)^2=225\)
Do đó: A=B
n=6 thì \(A=1^3+2^3+3^3+4^3+5^3+6^3=441\)
\(B=\left(1+2+3+4+5+6\right)^2=21^2=441\)
Do đó: A=B
TT
14 tháng 8 2020
Đề bài : Chứng minh rằng tổng lập phương của các số tự nhiên liên tiếp từ 1 đến n bằng bình phương của tổng từ 1 đến n ( n tự nhiên ). Hay ta cần chứng minh : \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) (*)
Lời giải :
+) Xét \(n=1\) thì ta có : \(1^3=1^2\) ( đúng )
Suy ra (*) đúng với \(n=1\) (1)
+) Xét \(n=2\) ta có : \(1^3+2^3=1+8=9\); \(\left(1+2\right)^2=3^2=9\)
\(\Rightarrow1^3+2^3=\left(1+2\right)^2\) ( đúng ). Nên (*) đúng với \(n=2\) (2)
+) Giả sử (*) đúng với \(n=k\). Tức là : \(1^3+2^3+3^3+....+k^3=\left(1+2+...+k\right)^2\).
Ta cần chứng minh \(n=k+1\) cũng đúng với (*). Thật vậy , ta có :
\(1^3+2^3+3^3+.....+\left(k+1\right)^3\)
\(=1^3+2^3+....+k^3+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+\left(k+1\right)^3\)
Xét biểu thức \(\left(k+1\right)^2+2.\left(k+1\right).\left(1+2+3+....+k\right)\)
\(=\left(k+1\right)^2+2.\left(k+1\right)\cdot\frac{\left(k+1\right).k}{2}\)
\(=\left(k+1\right)^2+\left(k+1\right)^2.k=\left(k+1\right)^3\)
Do đó \(1^3+2^3+....+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+2.\left(k+1\right)\left(1+2+....+k\right)+\left(k+1\right)^2\)
\(=\left(1+2+3+....+k+k+1\right)^2\)
Vậy (*) đúng với \(n=k+1\) (3)
Từ (1) (2) và (3) suy ra \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) với mọi \(n\in N\).
13 tháng 7 2023
Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
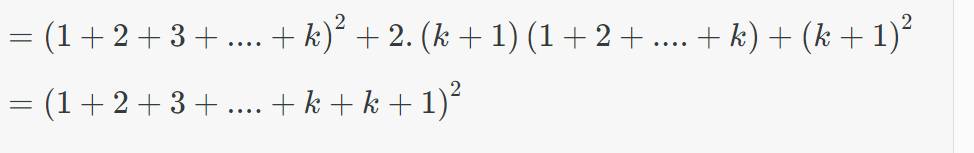
=>ĐPCM
NT
0
NT
2
QA
25 tháng 2 2016
bài 1:
Ta có:
1+2+3+...+2005≡(2005+1).2005:2≡2006.2005:2
≡1003.2005≡3.1≡3
(mod 4)
Vậy tổng của các số từ 1 đến 2005 có dạng 4k+3 (k∈N) nên không là số chính phương (đpcm)
Đây là toán lớp 7 mạ