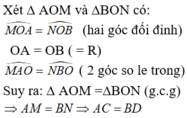Cho (O) đường kính AB, kẻ hai dây AC và BD song song với nhau.
a) Chứng minh AC= BD; b) Chứng minh 3 điểm C, O, D thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
20 tháng 1 2017
Đường thẳng qua O và vuông góc với AC và BD lần lượt tại H và K (H ∈ AC; KBD)
Ta có ∆AOH = ∆BOK (g.c.g) => AK = BK => AC = BD
KT
1
IM
10 tháng 9 2016
Ta có :
AC // BD
=> \(\begin{cases}\widehat{A_2}=\widehat{B_2}\\\widehat{C_2}=\widehat{D_2}\end{cases}\)
Từ giác ABCD nội tiếp đường tròn
=> \(\widehat{A_2}=\widehat{C_2}\)
\(\Rightarrow\widehat{A_2}=\widehat{B_2}=\widehat{C_2}=\widehat{D_2}\)
\(\Rightarrow\begin{cases}OA=OC\\OB=OD\end{cases}\)
Tương tự ta có \(\begin{cases}OA=OD\\OB=OC\end{cases}\)
\(\Rightarrow OA=OB=OC=OD\)
\(\Rightarrow AB=CD\)
CM
18 tháng 4 2019
Đáp án A
Qua O dựng đường thẳng vuông góc với AC và BD. Đường thẳng này cắt AC và BD lần lượt tại M và N.
