Gấp lắm ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{x}{27}=\dfrac{2}{9}-\dfrac{1}{3}\Rightarrow\dfrac{x}{27}=-\dfrac{1}{9}\Rightarrow\dfrac{x}{27}=\dfrac{-3}{27}\Rightarrow x=27\)
\(\dfrac{x}{27}=\dfrac{2}{9}-\dfrac{1}{3}=-\dfrac{1}{9}\Rightarrow x=-\dfrac{1}{9}.27=-3\).



\(a.2^{x+2}-2^x=96\\ 2^x\cdot4-2^x=96\\ 2^x\cdot\left(4-1\right)=96\\ 2^x\cdot3=96\\ 2^x=96:3\\ 2^x=32\\ 2^x=2^5\\ =>x=5\)
\(2^{x+1}\cdot3^y=12^x\\ 2^{x+1}\cdot3^y=3^x\cdot2^{2x}\\ \left\{{}\begin{matrix}2^{x+1}=2^{2x}\\3^y=3^x\end{matrix}\right.\\ \left\{{}\begin{matrix}x+1=2x\\y=x\end{matrix}\right.\\ \left\{{}\begin{matrix}x=1\\y=x=1\end{matrix}\right.\\ \left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
\(c.10^x:5^y=20^y\\ 10^x:5^y=5^y\cdot4^y\\ 10^x=10^{2y}\\ =>x=2y\)

MgO: Mg có điện hóa trị 2+, O có điện hóa trị 2-
FeF3: Fe có điện hóa trị 3+, F có điện hóa trị 1-
BaCl2: Ba có điện hóa trị 2+, Cl có điện hóa trị 1-
Ca3N2: Ca có điện hóa trị 2+, N có điện hóa trị 3-


a)\(4x^2+x=x\left(4x+1\right)\)
b)\(3x-9y=3\left(x-3y\right)\)
c)\(5\left(x-y\right)-x\left(x-y\right)=\left(5-x\right)\left(x-y\right)\)
d)\(4\left(2x-y\right)-x\left(y-2x\right)=-4\left(y-2x\right)-x\left(y-2x\right)=\left(-4-x\right)\left(y-2x\right)\)
e)\(\left(2x+1\right)^2+2\left(2x+1\right)=\left(2x+1\right)\left(2x+1+2\right)=\left(2x+1\right)\left(2x+3\right)\)
f)\(y\left(x+y\right)-y-x=y\left(x+y\right)-\left(x+y\right)=\left(y-1\right)\left(x+y\right)\)
g)\(2y\left(x-y\right)^2+x\left(y-x\right)^2=2y\left(y-x\right)^2+x\left(y-x\right)^2=\left(2y+x\right)\left(y-x\right)^2\)
h)

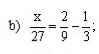


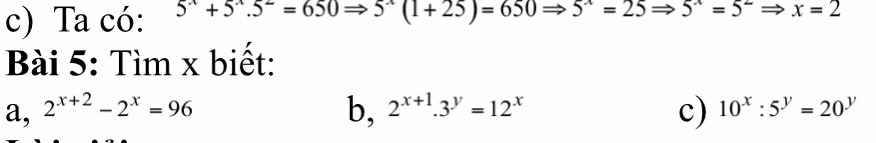





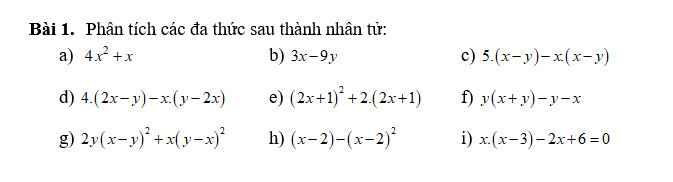
a) \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}.\left(\sqrt{x}-1\right)=\dfrac{x-1}{\sqrt{x}}\)
b) \(A=2\Rightarrow\dfrac{x-1}{\sqrt{x}}=2\Rightarrow x-1=2\sqrt{x}\Rightarrow x-2\sqrt{x}-1=0\)
\(\Rightarrow x-2\sqrt{x}+1=2\Rightarrow\left(\sqrt{x}-1\right)^2=2\Rightarrow\left[{}\begin{matrix}\sqrt{x}-1=\sqrt{2}\\\sqrt{x}-1=-\sqrt{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=\sqrt{2}+1\\\sqrt{x}=1-\sqrt{2}\left(l\right)\end{matrix}\right.\Rightarrow x=\left(\sqrt{2}+1\right)^2=3+2\sqrt{2}\)
c) \(A< 0\Rightarrow\dfrac{x-1}{\sqrt{x}}< 0\) mà \(\sqrt{x}>0\Rightarrow x-1< 0\Rightarrow x< 1\Rightarrow0< x< 1\)