Nhờ màn xem hộ câu 4 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 61:
a: \(B=\dfrac{3}{\sqrt{x}-2}+\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{x-4}\)
\(=\dfrac{3}{\sqrt{x}-2}+\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\left(\sqrt{x}+2\right)+4\left(\sqrt{x}-2\right)-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}+6+4\sqrt{x}-8-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{7\sqrt{x}-14}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{7\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{7}{\sqrt{x}+2}\)
b: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{3\sqrt{x}+1}{1-x}\)
\(=\dfrac{\left(\sqrt{x}+1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2+\left(\sqrt{x}-1\right)^2-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
Câu 60
Khi a=2 thì hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}\left(2^2-1\right)x+y=3\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=2x-7=2\cdot2-7=-3\end{matrix}\right.\)

Câu 1
- Chị ơi làm ơn mở cửa sổ giùm em
- Anh ơi mở cửa sổ giùm em
- Chị ơi nhờ chị mở cửa sổ cho em cái
- Anh ơi mở cửa sổ cho em cái
Câu2
- Bố ơi mấy giờ hai bố con ta đi thăm ông bà
- Bố ơi mấy giờ đi thăm ông bà
- Bố mấy giờ đi thăm ông bà
-
-
-
-

mình lm ở dưới r mà bạn
We will have a three-month vacation
từ gợi ý hình như sai






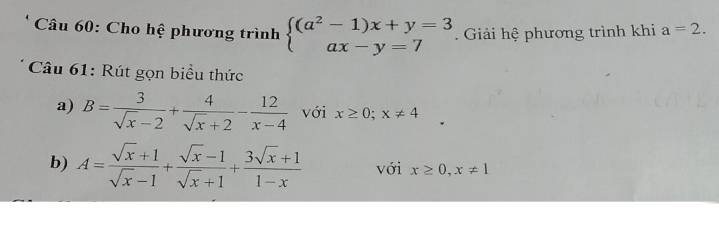
 mn xem hộ mk câu 14 ạ
mn xem hộ mk câu 14 ạ 
a, Xét △AHC và △BAC có:
∠BAC=∠AHC (=90o) , ∠ACB chung
⇒ △AHC ∼ △BAC (g.g)
b, Ta có: ∠BAC=∠ADH=∠AIH (=90o)
⇒ tứ giác ADHI là hcn ⇒ DI=AH
c, Xét △ADH và △AHB có:
∠BAH chung , ∠AHB=∠ADH (=90o)
⇒ △ADH ∼ △AHB (g.g)
⇒ \(\dfrac{AD}{AH}=\dfrac{AH}{AB}\) ⇒ AH2=AD.AB (1)
Xét △AIH và △AHC có:
∠HAC chung , ∠AHC=∠AIH (=90o)
⇒ △AIH ∼ △AHC (g.g)
⇒ \(\dfrac{AI}{AH}=\dfrac{AH}{AC}\) ⇒ AH2=AI.AC (2)
Từ (1) và (2) ⇒ AI.AC=AD.AB ⇒ \(\dfrac{AI}{AD}=\dfrac{AC}{AB}\)
Xét △ADI và △ABC có:
∠BAC chung (=90o), \(\dfrac{AI}{AD}=\dfrac{AC}{AB}\) (cmt)
⇒ △ADI và △ABC (c.g.c)