Cho hai số không âm a và b. Ta gọi trung bình nhân của hai số a và b và \(\sqrt{ab}\). Chứng minh rằng trung bình cộng của hai số a và b không nhỏ hơn trung bình nhân của chúng (bất đẳng thức của Côsi).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

5 tháng 3 2017
Tổng của của 3 số là : 45 + 52 + 48 = 145
Tổng của A và B là : 45 * 2 = 90
Tổng của C và D là :48 * 2 = 96
Số D là : 145 - 96 = 49
Số A là : 145 - 90 = 55
TBC của A và D là : [ 55 + 49 ] : 2 = 52
Đáp số : 52

22 tháng 6 2021
Biết trung bình cộng của hai số A và B là 29, trung bình cộng của hai số B và C là 25, trung bình cộng của hai số C và D là 27. Trung bình cộng của hai số A và D

4 tháng 3 2017
/+95795654974764579457625179457645761879546841549184*918794567541159745672389752789123*9856239456123594613961356623231333366548525215632
4 tháng 3 2017
4175120741741852784518585639+658233629653
856238562385623895623
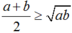
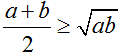
Ta cần c/m: \(\dfrac{a+b}{2}\ge\sqrt{ab}\left(1\right)\) (a;b ≥ 0)
Thật vậy:
\(\left(1\right)\Leftrightarrow\left(\dfrac{a+b}{2}\right)^2\ge ab\\ \Leftrightarrow\dfrac{a^2+2ab+b^2}{4}\ge ab\\ \Leftrightarrow a^2+2ab+b^2\ge4ab\\ \Leftrightarrow a^2-2ab+b^2\ge0\\ \Leftrightarrow\left(a-b\right)^2\ge0\left(\text{luôn đúng }\forall a;b\ge0\right)\)
Vậy BĐT Cô-si cho 2 số không âm được c/m.