Tìm x < 0, biết 3x2 = 675.
Tìm x.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3x2 +15x = 0
3x( x + 5 ) = 0
TH1: 3x = 0
x = 0 : 3
x = 0
TH2: x + 5 = 0
x = 0 - 5
x = -5
Vậy x ∈ { 0; -5 }

Ta có
x 3 + 3 x 2 + 3 x + 1 = 0 ⇔ ( x + 1 ) 3 = 0
ó x + 1 = 0 ó x = -1
Vậy x = -1
Đáp án cần chọn là: A

b) Ta có: 5x3 – 3x2 + 10x – 6 = (5x3 + 10x )+ ( -3x2– 6)
= 5x(x2 + 2) – 3(x2 + 2) = (x2 + 2)(5x – 3)
Vậy (x2 + 2)(5x – 3) = 0 ⇒ 5x – 3 = 0 (vì x2 + 2 ≥ 0, với mọi x)
⇒x = 3/5

\(\left(3x^2+x\right)^2+\left(3x^2+x\right)-2\left(3x^2+x\right)-2=0\)
\(\Leftrightarrow\left(3x^2+x\right)\left(3x^2+x+1\right)-2\left(3x^2+x+1\right)=0\)
\(\Leftrightarrow\left(3x^2+x-2\right)\left(3x^2+x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x-2\right)\left[3\left(x+\dfrac{1}{6}\right)^2+\dfrac{11}{12}\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{2}{3}\end{matrix}\right.\)

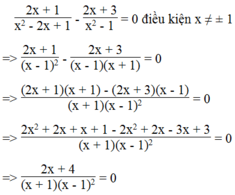
Biểu thức bằng 0 khi tử bằng 0 và mẫu khác 0
Ta có: 2x + 4 = 0 => x = - 2 (thỏa mãn điều kiện)
Vậy với x = - 2 thì giá trị của biểu thức bằng 0.

\(a,\Leftrightarrow\left(x-4\right)\left(x^2+5\right)>0\\ \Leftrightarrow x-4>0\left(x^2+5\ge5>0\right)\\ \Leftrightarrow x>4\\ b,\Leftrightarrow\left(x-y\right)\left(3x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=y\left(vô.lí.do.x\ne y\right)\\x=\dfrac{5}{3}\left(tm\right)\end{matrix}\right.\\ \Leftrightarrow S=x^2-x=\dfrac{25}{9}-\dfrac{5}{3}=\dfrac{10}{9}\)
theo bài ra, có 3x2=675
=> x2=675:3
=> x2=225
=> x=\(\sqrt{225}\)
=> x= 15 hoặc x=-15
mà theo bài ra x<0 nên x=-15
vậy x=-15