Em đang cần gấp ạ,hạn là 11h🥺🥺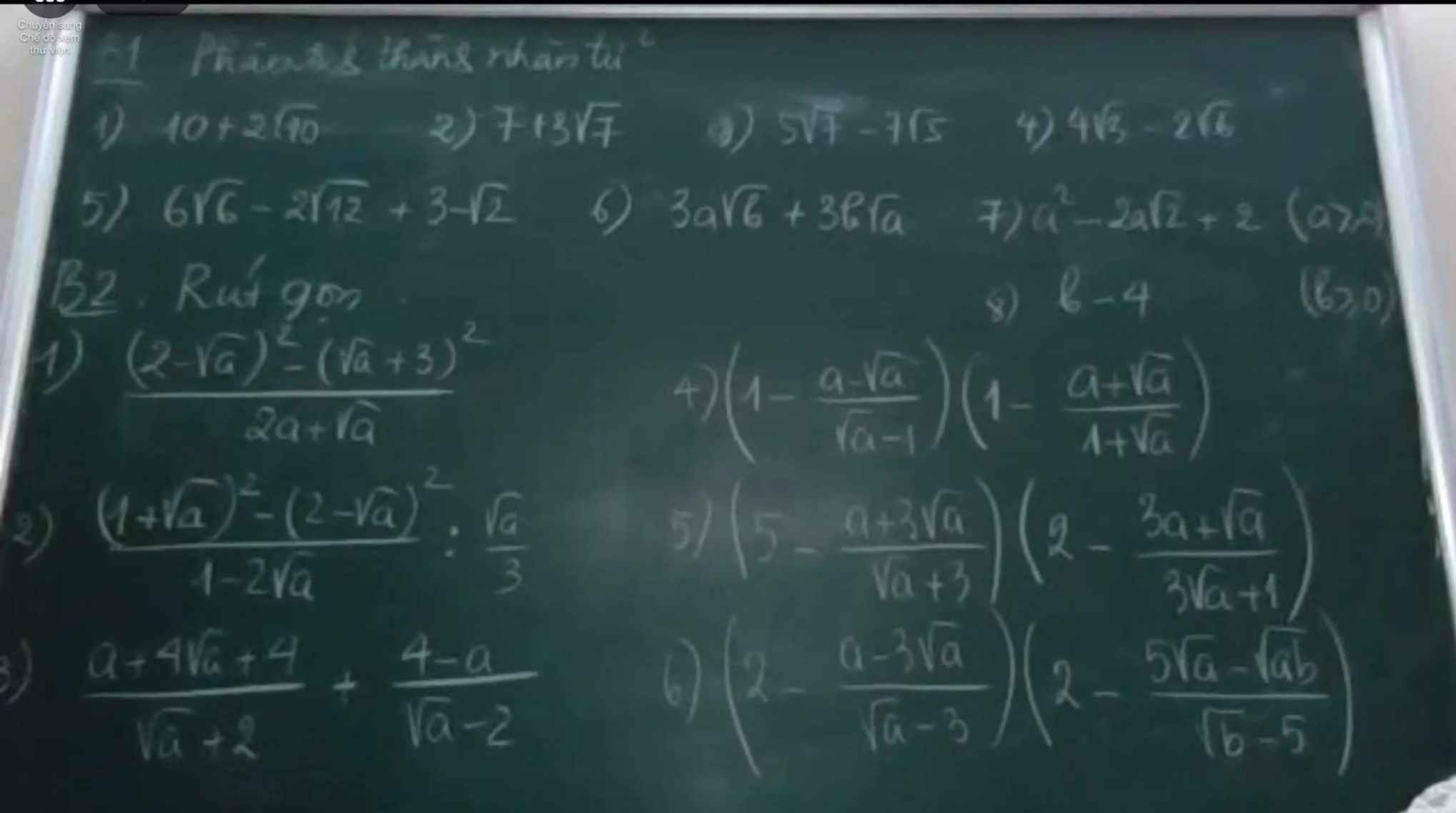
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình xin không viết lại điều kiện , tại đề có rồi
\(A=\left(\dfrac{a\sqrt{a}+b\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right)\left(\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}\right)=\left(a+b-\sqrt{ab}-\sqrt{ab}\right)\cdot\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}\\ =\left(\sqrt{a}-\sqrt{b}\right)^2\cdot\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)=a-b\)\(B=\left(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\sqrt{ab}\right):\left(\sqrt{a}+\sqrt{b}\right)^2=\left(a+b+\sqrt{ab}+\sqrt{ab}\right):\left(\sqrt{a}+\sqrt{b}\right)^2=\left(\sqrt{a}+\sqrt{b}\right)^2:\left(\sqrt{a}+\sqrt{b}\right)^2=1\)
\(C=\dfrac{x-y}{\sqrt{x}-\sqrt{y}}-\dfrac{\sqrt{x^3}-\sqrt{y^3}}{x+\sqrt{xy}+y}-2\sqrt{y}=\sqrt{x}+\sqrt{y}-\left(\sqrt{x}-\sqrt{y}\right)-2\sqrt{y}=0\)
a) Ta có: \(A=\left(\dfrac{a\sqrt{a}+b\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right)\cdot\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}\)
\(=\left(a-\sqrt{ab}+b-\sqrt{ab}\right)\cdot\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}\)
\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)\)
=a-b
b) Ta có: \(B=\left(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\sqrt{ab}\right):\left(\sqrt{a}+\sqrt{b}\right)^2\)
\(=\left(a+\sqrt{ab}+\sqrt{ab}+b\right):\left(\sqrt{a}+\sqrt{b}\right)^2\)
\(=1\)
c) Ta có: \(C=\dfrac{x-y}{\sqrt{x}-\sqrt{y}}-\dfrac{\sqrt{x^3}-\sqrt{y^3}}{x+\sqrt{xy}+y}-2\sqrt{y}\)
\(=\sqrt{x}+\sqrt{y}-\sqrt{x}+\sqrt{y}-2\sqrt{y}\)
=0

a) Vì ABCD là hình bình hành ( gt )
⇒ AD // BC
F ∈ BC
⇒ AD // BF
⇒ ∠EDA = ∠EFB ( hai góc so le trong )
Xét △AED và △BEF, có :
∠EDA = ∠EFB ( cmt )
∠AED = ∠FEB ( hai góc đối đỉnh )
⇒ △AED ∼ △BEF (g-g)
b) Vì ABCD là hình bình hành ( gt )
⇒ AB // CD
E ∈ AB
⇒ BE // CD
Xét △FDC, có :
BE // CD ( cmt )
E ∈ DF ; B ∈ DC
⇒ \(\dfrac{FB}{FC}=\dfrac{EB}{DC}\) (Hệ quả của định lí Ta-let)
⇒ \(\dfrac{BF}{BE}=\dfrac{FC}{DC}\) (1)
Vì △AED ∼ △BEF ( cmt )
⇒ \(\dfrac{AE}{BE}=\dfrac{AD}{BF}\) (TSDD)
⇒ \(\dfrac{AE}{AD}=\dfrac{BE}{BF}\) (2)
Từ (1) và (2) ⇒ \(\dfrac{AE}{AD}=\dfrac{CF}{CD}\)
⇒ AD.CD = AE.CF
c) Xét △DGC, có :
AE // DC ( cmt )
G ∈ AC ; G ∈ DE
⇒ \(\dfrac{DG}{DE}=\dfrac{GC}{AC}\) (Hệ quả của định lí Ta-let) (3)
Xét △FGC, có :
AD // CF ( cmt )
G ∈ AC ; G ∈ DF
⇒ \(\dfrac{DG}{DF}=\dfrac{AG}{AC}\) (Hệ quả của định lí Ta-let) (4)
Từ (3) và (4) ⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}=\dfrac{GC}{AC}+\dfrac{AG}{AC}\)
⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}\) = 1
⇒ \(\dfrac{1}{DG}\left(\dfrac{DG}{DE}+\dfrac{DG}{DF}\right)=\dfrac{1}{DG}\)
⇒ \(\dfrac{1}{DG}=\dfrac{1}{DE}+\dfrac{1}{DF}\)

\(a,=\sqrt{x^3}-1=x\sqrt{x}-1\\ b,=\sqrt{x^3}-\sqrt{y^3}=x\sqrt{x}-y\sqrt{y}\\ c,=8\sqrt{x^3}+\sqrt{y^3}=2x\sqrt{x}+y\sqrt{y}\)
a) \(\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)=\left(\sqrt{x}\right)^3-1=x\sqrt{x}-1\)
b) \(\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{x}.\sqrt{y}+y\right)=\left(\sqrt{x}\right)^3+\left(\sqrt{y}\right)^3=x\sqrt{x}+y\sqrt{y}\)
c) \(\left(2\sqrt{x}+\sqrt{y}\right)\left(3\sqrt{x}-2\sqrt{y}\right)=6x-4\sqrt{xy}+3\sqrt{xy}-2y=6x-\sqrt{xy}-2y\)




a: 2+5/6=12/6+5/6=17/6
b: 5/12+3/4+1/3=5/12+9/12+4/12=18/12=3/2
c: 2/3+3/4=8/12+9/12=17/12

4b.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\left(\dfrac{\pi}{3}\right)}{1-tana.tan\left(\dfrac{\pi}{3}\right)}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=...\)
c.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{5}{13}\)
\(cos\left(\dfrac{\pi}{3}-a\right)=cos\left(\dfrac{\pi}{3}\right).cosa+sin\left(\dfrac{\pi}{3}\right).sina=\dfrac{1}{2}.\dfrac{5}{13}+\left(-\dfrac{12}{13}\right).\dfrac{\sqrt{3}}{2}=...\)
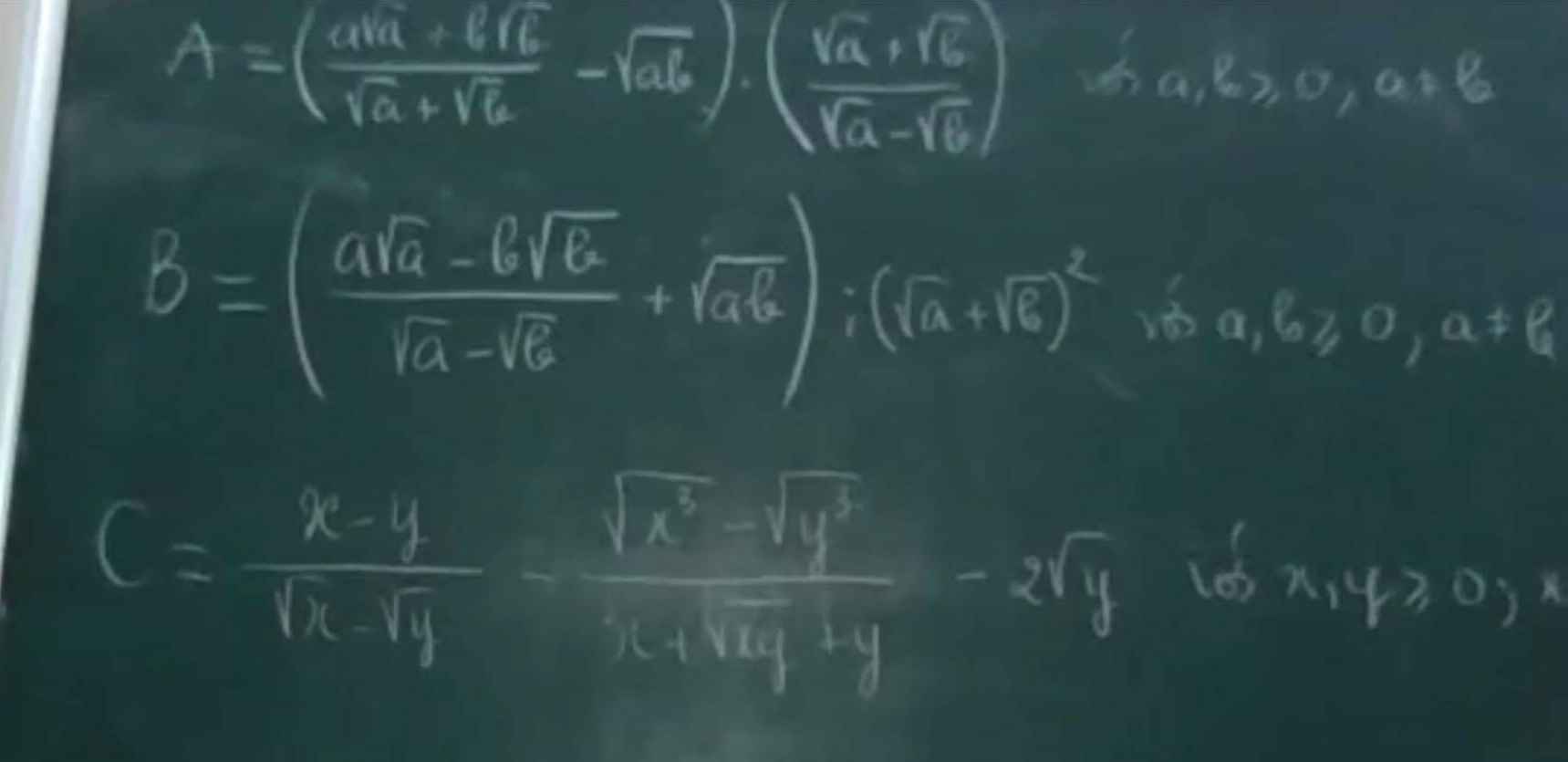

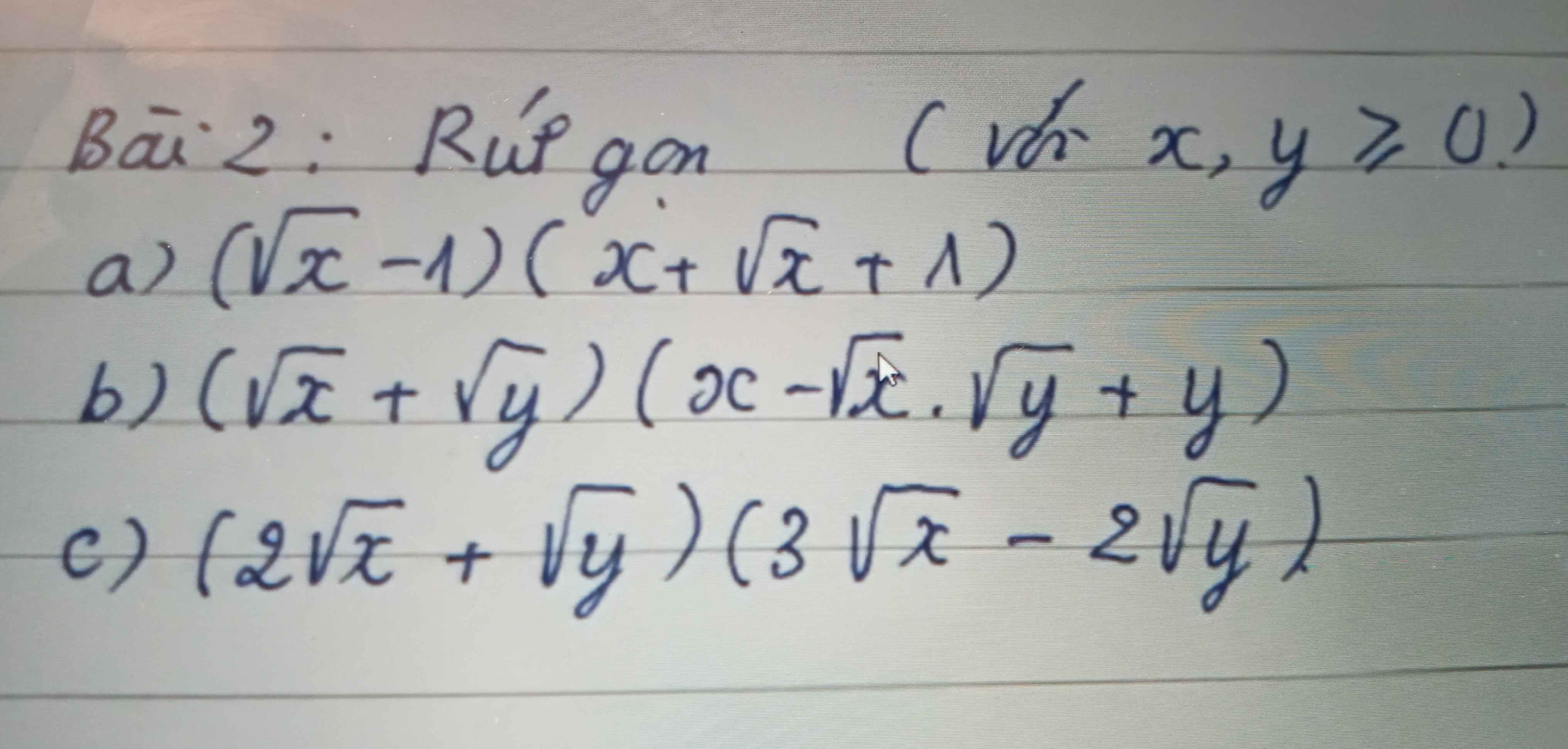






Bài 1:1) \(10+2\sqrt{10}=\sqrt{10}\left(2+\sqrt{10}\right)\)
2) \(7+3\sqrt{7}=\sqrt{7}\left(3+\sqrt{7}\right)\)
các câu 3,4,5 bạn làm tương tự như 2 câu trên
6) \(3a\sqrt{b}+3b\sqrt{a}=3\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)\)
7) \(a^2-2a\sqrt{2}+2=a^2-2a\sqrt{2}+\left(\sqrt{2}\right)^2=\left(a-\sqrt{2}\right)^2\)
8) \(b-4=\left(\sqrt{b}\right)^2-2^2=\left(\sqrt{b}-2\right)\left(\sqrt{b}+2\right)\)
Bài 2: 1) \(\dfrac{\left(2-\sqrt{a}\right)^2-\left(\sqrt{a}+3\right)^2}{2a+\sqrt{a}}\left(a>0\right)\)
\(=\dfrac{\left(2-\sqrt{a}-\sqrt{a}-3\right)\left(2-\sqrt{a}+\sqrt{a}+3\right)}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=\dfrac{\left(-2\sqrt{a}-1\right).5}{\sqrt{a}\left(2\sqrt{a}+1\right)}=-\dfrac{5}{\sqrt{a}}\)
3) \(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\left(a\ge0,a\ne4\right)\)
\(=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}=\sqrt{a}+2-\left(2+\sqrt{a}\right)=0\)
4) \(\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\left(a\ge0,a\ne1\right)\)
\(=\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{1+\sqrt{a}}\right)\)
\(=\left(1-\sqrt{a}\right)\left(1-\sqrt{a}\right)=\left(1-\sqrt{a}\right)^2=a-2\sqrt{a}+1\)
mấy câu còn lại bạn làm tương tự
Bài 1:
1) \(10+2\sqrt{10}=2\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)\)
2) \(7+3\sqrt{7}=\sqrt{7}\left(\sqrt{7}+3\right)\)
3) \(5\sqrt{7}-7\sqrt{5}=\sqrt{35}\left(\sqrt{5}-\sqrt{7}\right)\)
4) \(4\sqrt{3}-2\sqrt{6}=2\sqrt{6}\left(\sqrt{2}-\sqrt{1}\right)\)
5) \(6\sqrt{6}-2\sqrt{12}+3\sqrt{2}\)
\(=\sqrt{216}-\sqrt{48}+\sqrt{18}\)
\(=\sqrt{6}\left(6-2\sqrt{2}+\sqrt{3}\right)\)
6) \(3a\sqrt{6}+36\sqrt{a}\)
\(=3\sqrt{a}\left(\sqrt{6a}+12\right)\)
\(=3\sqrt{6a}\left(\sqrt{a}+2\sqrt{6}\right)\)
7) \(a^2-2a\sqrt{2}+2=\left(a-\sqrt{2}\right)^2\)
8) \(b-4=\left(\sqrt{b}-2\right)\left(\sqrt{b}+2\right)\)
Bài 2:
a) Ta có: \(\dfrac{\left(2-\sqrt{a}\right)^2-\left(\sqrt{a}+3\right)^2}{2a+\sqrt{a}}\)
\(=\dfrac{a-4\sqrt{a}+4-a-6\sqrt{a}-9}{2a+\sqrt{a}}\)
\(=\dfrac{-10\sqrt{a}-5}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=\dfrac{-5\left(2\sqrt{a}+1\right)}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=-\dfrac{5}{\sqrt{a}}\)
4) Ta có: \(\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\)
\(=\left(1-\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
\(=a-2\sqrt{a}+1\)