
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:1) \(10+2\sqrt{10}=\sqrt{10}\left(2+\sqrt{10}\right)\)
2) \(7+3\sqrt{7}=\sqrt{7}\left(3+\sqrt{7}\right)\)
các câu 3,4,5 bạn làm tương tự như 2 câu trên
6) \(3a\sqrt{b}+3b\sqrt{a}=3\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)\)
7) \(a^2-2a\sqrt{2}+2=a^2-2a\sqrt{2}+\left(\sqrt{2}\right)^2=\left(a-\sqrt{2}\right)^2\)
8) \(b-4=\left(\sqrt{b}\right)^2-2^2=\left(\sqrt{b}-2\right)\left(\sqrt{b}+2\right)\)
Bài 2: 1) \(\dfrac{\left(2-\sqrt{a}\right)^2-\left(\sqrt{a}+3\right)^2}{2a+\sqrt{a}}\left(a>0\right)\)
\(=\dfrac{\left(2-\sqrt{a}-\sqrt{a}-3\right)\left(2-\sqrt{a}+\sqrt{a}+3\right)}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=\dfrac{\left(-2\sqrt{a}-1\right).5}{\sqrt{a}\left(2\sqrt{a}+1\right)}=-\dfrac{5}{\sqrt{a}}\)
3) \(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\left(a\ge0,a\ne4\right)\)
\(=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}=\sqrt{a}+2-\left(2+\sqrt{a}\right)=0\)
4) \(\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\left(a\ge0,a\ne1\right)\)
\(=\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{1+\sqrt{a}}\right)\)
\(=\left(1-\sqrt{a}\right)\left(1-\sqrt{a}\right)=\left(1-\sqrt{a}\right)^2=a-2\sqrt{a}+1\)
mấy câu còn lại bạn làm tương tự
Bài 1:
1) \(10+2\sqrt{10}=2\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)\)
2) \(7+3\sqrt{7}=\sqrt{7}\left(\sqrt{7}+3\right)\)
3) \(5\sqrt{7}-7\sqrt{5}=\sqrt{35}\left(\sqrt{5}-\sqrt{7}\right)\)
4) \(4\sqrt{3}-2\sqrt{6}=2\sqrt{6}\left(\sqrt{2}-\sqrt{1}\right)\)
5) \(6\sqrt{6}-2\sqrt{12}+3\sqrt{2}\)
\(=\sqrt{216}-\sqrt{48}+\sqrt{18}\)
\(=\sqrt{6}\left(6-2\sqrt{2}+\sqrt{3}\right)\)
6) \(3a\sqrt{6}+36\sqrt{a}\)
\(=3\sqrt{a}\left(\sqrt{6a}+12\right)\)
\(=3\sqrt{6a}\left(\sqrt{a}+2\sqrt{6}\right)\)
7) \(a^2-2a\sqrt{2}+2=\left(a-\sqrt{2}\right)^2\)
8) \(b-4=\left(\sqrt{b}-2\right)\left(\sqrt{b}+2\right)\)
Bài 2:
a) Ta có: \(\dfrac{\left(2-\sqrt{a}\right)^2-\left(\sqrt{a}+3\right)^2}{2a+\sqrt{a}}\)
\(=\dfrac{a-4\sqrt{a}+4-a-6\sqrt{a}-9}{2a+\sqrt{a}}\)
\(=\dfrac{-10\sqrt{a}-5}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=\dfrac{-5\left(2\sqrt{a}+1\right)}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=-\dfrac{5}{\sqrt{a}}\)
4) Ta có: \(\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\)
\(=\left(1-\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
\(=a-2\sqrt{a}+1\)



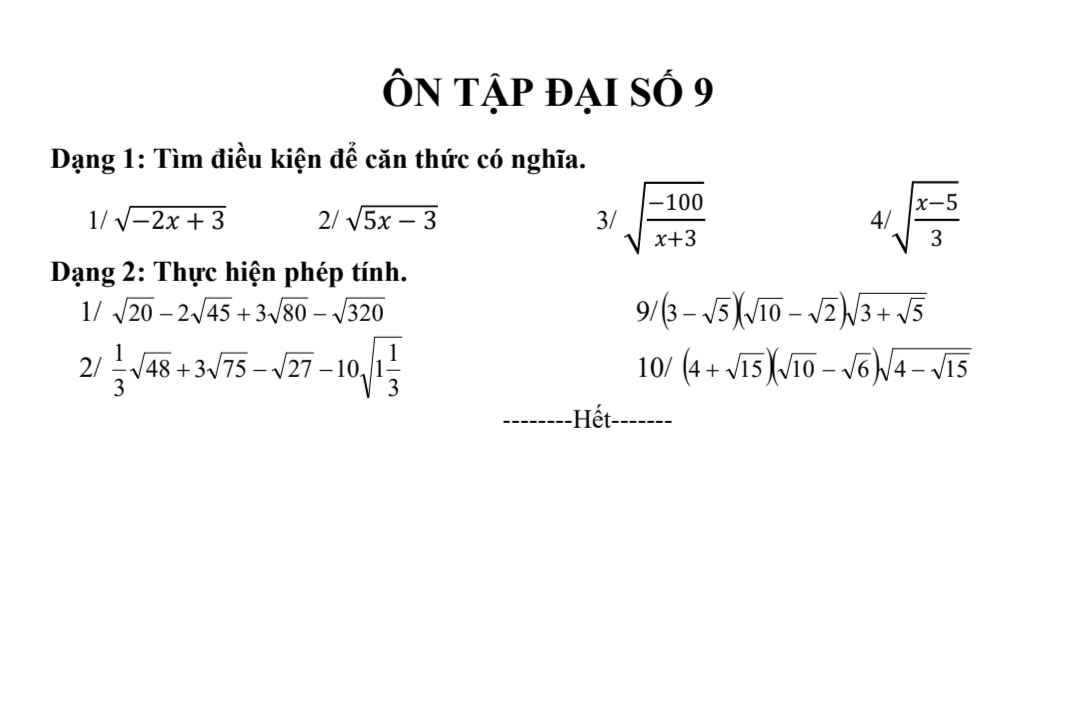
Dạng 1:
1/ ĐKXĐ: \(x\le0\)
2/ ĐKXĐ: \(x\ge\dfrac{3}{5}\)
3/ ĐKXĐ: \(x\le-4\)
4/ ĐKXĐ: \(x\ge5\)
Dạng 1:
\(1,ĐK:-2x+3\ge0\Leftrightarrow x\le\dfrac{3}{2}\\ 2,ĐK:5x-3\ge0\Leftrightarrow x\ge\dfrac{3}{5}\\ 3,ĐK:\dfrac{-100}{x+3}\ge0\Leftrightarrow x+3< 0\left(-100< 0;x+3\ne0\right)\\ \Leftrightarrow x< -3\\ 4,ĐK:\dfrac{x-5}{3}\ge0\Leftrightarrow x-5\ge0\left(3>0\right)\\ \Leftrightarrow x\ge5\)
Dạng 2:
\(1,=2\sqrt{5}-6\sqrt{5}+12\sqrt{5}-8\sqrt{5}=0\\ 9,=\left(3-\sqrt{5}\right)\left(\sqrt{5}-1\right)\sqrt{6+2\sqrt{5}}\\ =\left(3-\sqrt{5}\right)\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)\\ =4\left(3-\sqrt{5}\right)=12-4\sqrt{5}\\ 2,=\dfrac{4\sqrt{3}}{3}+15\sqrt{3}-3\sqrt{3}-\dfrac{20\sqrt{3}}{3}\\ =12\sqrt{3}-\dfrac{16\sqrt{3}}{3}=\dfrac{36\sqrt{3}-16\sqrt{3}}{3}=\dfrac{20\sqrt{3}}{3}\\ 10,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)


1) ĐKXĐ: \(x\ge0\)
2) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
3) ĐKXĐ: \(x\ge4\)
4) ĐKXĐ: \(x>16\)
5) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge0\end{matrix}\right.\)
6) ĐKXĐ: \(\left[{}\begin{matrix}x\le-1\\x\ge4\end{matrix}\right.\)
7) ĐKXĐ: \(\left[{}\begin{matrix}1\le x\\x< 3\end{matrix}\right.\)
8) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x>3\end{matrix}\right.\)
9) ĐKXĐ: \(x\in R\)
10) ĐKXĐ: \(x\in R\)
11) ĐKXĐ: \(x\in R\)
12) ĐKXĐ: \(x\in R\)
13) ĐKXĐ: \(x\in R\)
14) ĐKXĐ: \(x\in R\)
15) ĐKXĐ: \(x\in R\)
16) ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
17) ĐKXĐ: \(x\ge7\)
18) ĐKXĐ: \(x\ge-5\)

Bài 1:
a: Ta có: \(P=\dfrac{\sqrt{a}+2}{\sqrt{a}+3}-\dfrac{5}{a+\sqrt{a}-6}-\dfrac{1}{\sqrt{a}-2}\)
\(=\dfrac{a-4-5-\sqrt{a}-3}{\left(\sqrt{a}+3\right)\left(\sqrt{a}-2\right)}\)
\(=\dfrac{\sqrt{a}-4}{\sqrt{a}-2}\)


a: \(2\sqrt{45}+\sqrt{5}-3\sqrt{80}\)
\(=6\sqrt{5}+\sqrt{5}-12\sqrt{5}\)
\(=-5\sqrt{5}\)
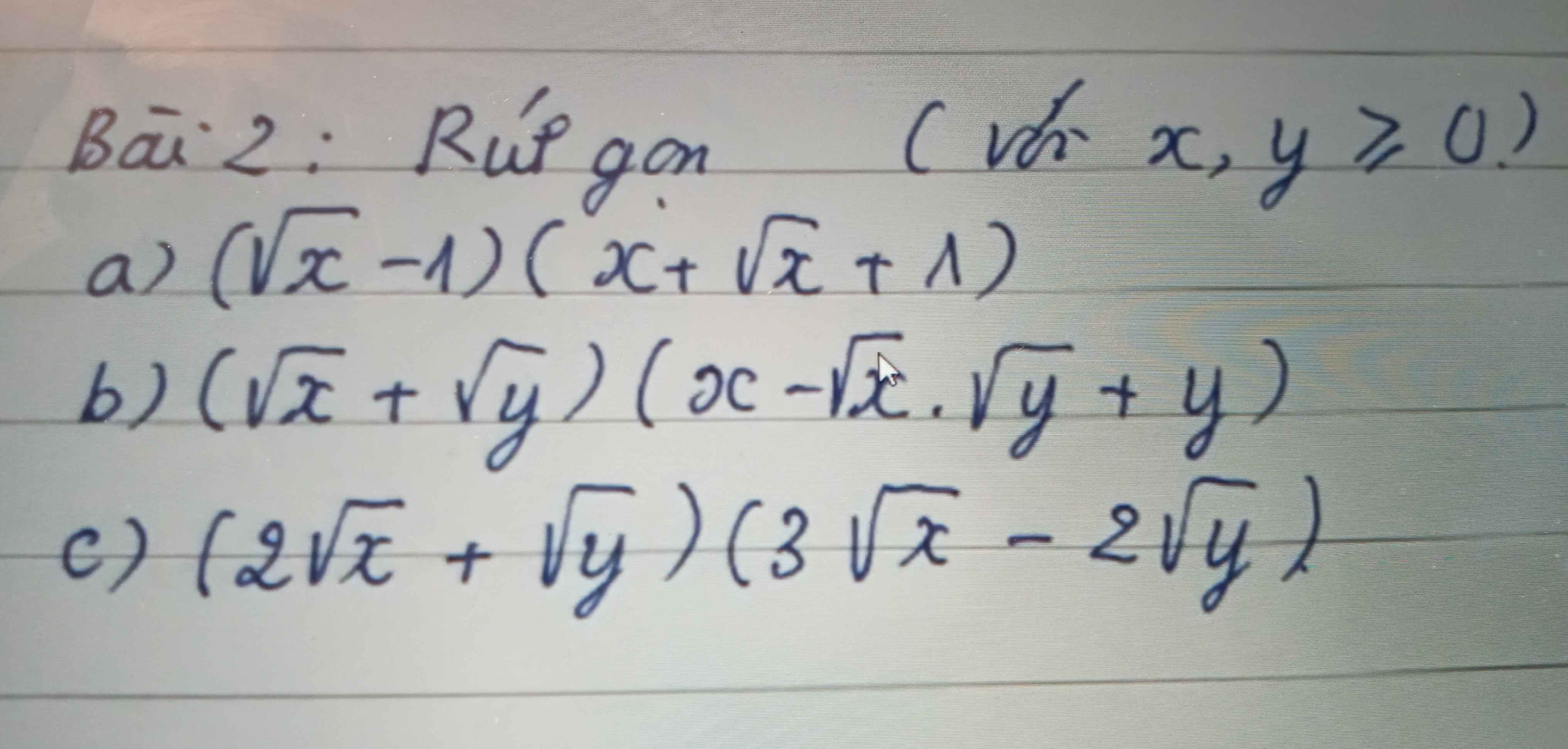
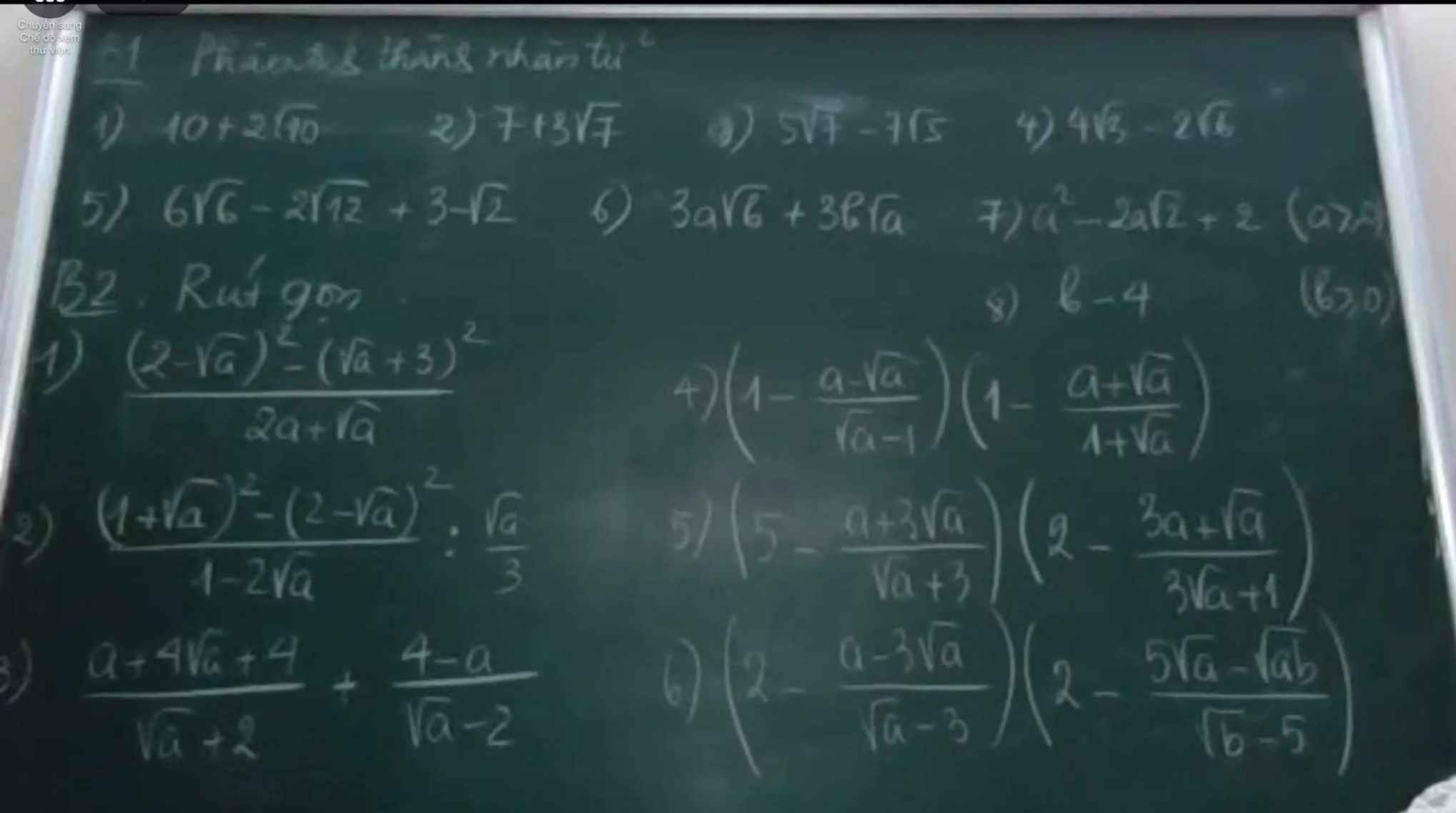


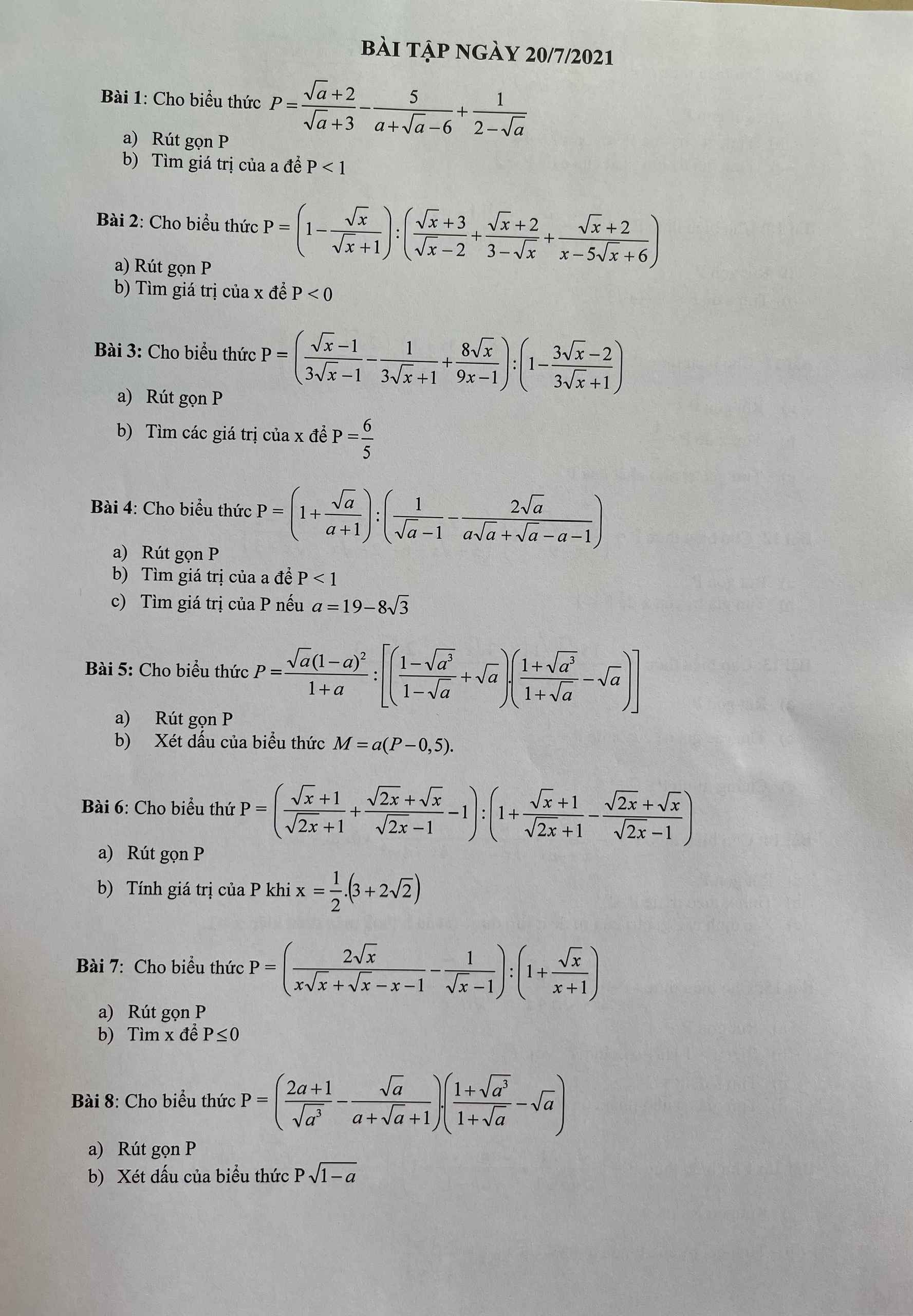 Gíup em với em đang cần gấp ạ^^
Gíup em với em đang cần gấp ạ^^
\(a,=\sqrt{x^3}-1=x\sqrt{x}-1\\ b,=\sqrt{x^3}-\sqrt{y^3}=x\sqrt{x}-y\sqrt{y}\\ c,=8\sqrt{x^3}+\sqrt{y^3}=2x\sqrt{x}+y\sqrt{y}\)
a) \(\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)=\left(\sqrt{x}\right)^3-1=x\sqrt{x}-1\)
b) \(\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{x}.\sqrt{y}+y\right)=\left(\sqrt{x}\right)^3+\left(\sqrt{y}\right)^3=x\sqrt{x}+y\sqrt{y}\)
c) \(\left(2\sqrt{x}+\sqrt{y}\right)\left(3\sqrt{x}-2\sqrt{y}\right)=6x-4\sqrt{xy}+3\sqrt{xy}-2y=6x-\sqrt{xy}-2y\)