Giải giúp mik 2 bài này trog tối nay ạ 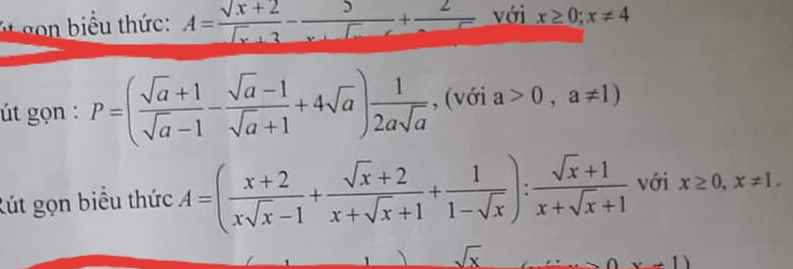
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


uses crt;
var st:string;
d,i,t,x,y,a,b:integer;
begin
clrscr;
readln(st);
d:=length(st);
for i:=1 to d do write(st[i]:4);
writeln;
t:=0;
for i:=1 to d do
begin
val(st[i],x,y);
t:=t+x;
end;
writeln(t);
val(st[d],a,b);
if (a mod 2=0) then write(1)
else write(-1);
readln;
end.

#include <bits/stdc++.h>
using namespace std;
long long a[1000],i,n,t,dem,t1;
int main()
{
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
t=0;
for (i=1; i<=n; i++) if (a[i]%2==0) t+=a[i];
cout<<t<<endl;
t1=0;
dem1=0;
for (i=1; i<=n; i++)
if (a[i]<0)
{
cout<<a[i]<<" ";
t1+=a[i];
dem1++;
}
cout<<endl;
cout<<fixed<<setprecision(1)<<(t1*1.0)/(dem1*1.0);
return 0;
}

#include <bits/stdc++.h>
using namespace std;
long long a,b;
//chuongtrinhcon
long long gcd(long long a,long long b)
{
if (b==0) return(a);
return gcd(b,a%b);
}
//chuongtrinhchinh
int main()
{
cin>>a>>b;
cout<<max(a,b)<<endl;
cout<<gcd(a,b)<<endl;
if ((a>0 && b>0) or (a<0 && b<0)) cout<<a/gcd(a,b)<<" "<<b/gcd(a,b);
else cout<<"-"<<-a/gcd(-a,b)<<" "<<b/gcd(-a,b);
return 0;
}

Nữa chu vi là
100:2=50 (cm)
CHiều dài là
50 : ( 2+3) x 3 = 30 (cm)
Chiều rộng là
50-30 = 20 (cm)
Diện tích hình chữ nhật là
20x30= 600 (cm2)

Số bé nhất có 3 chữ số là : 100
Số Bình nghĩ ra là : 100 - 15 = 85
Vậy số Bình nghĩ ra là số 85
Đáp số : 85

Bài `1`
\(a,A=a\left(a+b\right)-b\left(a+b\right)\\ =\left(a+b\right)\left(a-b\right)\)
Với `a=9;=10`
Ta có :
\(\left(a+b\right)\left(a-b\right)\\=\left(9+10\right)\left(9-10\right)\\ =19.\left(-1\right)\\ =-19\)
\(b,B=\left(3x+2\right)^2+\left(3x-2\right)^2-2\left(3x+2\right)\left(3x-2\right)\\ =\left(3x+2\right)^2-2\left(3x+2\right)\left(3x-2\right)+\left(3x-2\right)^2\\ =\left[\left(3x+2\right)-\left(3x-2\right)\right]^2\)
Với `x=-4`
Ta có :
\(\left[\left(3x+2\right)-\left(3x-2\right)\right]^2\\ =\left(3.4+2-3.4+2\right)^2\\ =\left(12+2-12+2\right)^2\\ =4^2\\ =16\)
\(2,\\ x^3-6x^2+9x\\ =x\left(x^2-6x+9\right)\\ =x\left(x-3\right)^2\\ x^2-2x-4y^2-4y\\ \)
`->` có đúng đề ko cậu
2:
b; x^2-4y^2-2x-4y
=(x-2y)*(x+2y)-2(x+2y)
=(x+2y)(x-2y-2)
a: x^3-6x^2+9x
=x(x^2-6x+9)
=x(x-3)^2

\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)

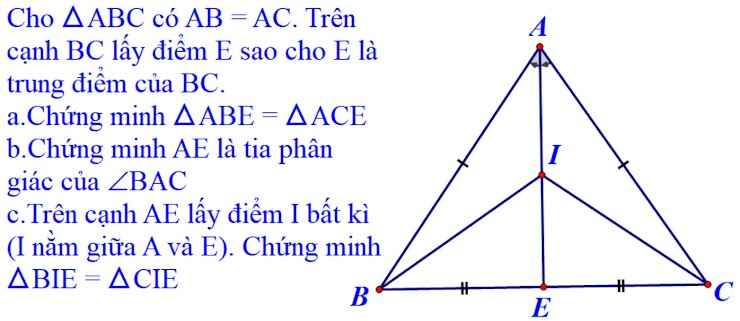
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).




 Mn ơi, giải hộ mik câu này với! Tối nay mik phải nộp rồi ạ! Cảm ơn mn nhiều lắm!
Mn ơi, giải hộ mik câu này với! Tối nay mik phải nộp rồi ạ! Cảm ơn mn nhiều lắm!

\(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\left[\dfrac{x+2}{\sqrt{x^3}-1}+\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x^3}-1}-\dfrac{x+\sqrt{x}+1}{\sqrt{x^3}-1}\right]:\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\left(\dfrac{x+2+x-\sqrt{x}+2\sqrt{x}-2-x-\sqrt{x}-1}{\sqrt{x^3}-1}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\dfrac{x-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}\)
\(=1\)
\(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right).\dfrac{1}{2a\sqrt{a}}\)
\(=\left[\dfrac{\left(\sqrt{a}+1\right)^2}{a-1}-\dfrac{\left(\sqrt{a}-1\right)^2}{a-1}+\dfrac{4\sqrt{a}\left(a-1\right)}{a-1}\right].\dfrac{1}{2a\sqrt{a}}\)
\(=\left(\dfrac{a+2\sqrt{a}+1-a+2\sqrt{a}-1+4a\sqrt{a}-4\sqrt{a}}{a-1}\right).\dfrac{1}{2a\sqrt{a}}\)
\(=\dfrac{4a\sqrt{a}}{a-1}.\dfrac{1}{2a\sqrt{a}}\)
\(=\dfrac{2}{a-1}\)