Cho bốn điểm A;B;C;D.Hãy vẽ các đường thẳng qua bốn điểm đó.
a)Có bao nhiêu trường hợp?Hãy vẽ hình mỗi trường hợp.
b)Trường hợp nào có số đường thẳng ít nhất?
c)Trường hợp nào có số đường thẳng nhiều nhất?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Ta có:
\(\left. \begin{array}{l}J \in C{\rm{D}}\\C{\rm{D}} \subset \left( {IC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {IC{\rm{D}}} \right)\).
Vậy bốn điểm \(I,J,C,D\) đồng phẳng.
Chọn D.
25 tháng 10 2019
giúp mk nhé mk cần gấp . ai lm xong trước và chuẩn nhất mk cho
25 tháng 10 2019
a)
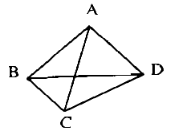
Vẽ được 6 đoạn thẳng
Tên đoạn thẳng: AB, BC, CD, AD, BD, AC
Read more: https://sachbaitap.com/cau-37-trang-130-sach-bai-tap-sbt-toan-6-tap-1-c8a5966.html#ixzz63N4AsIky
7 tháng 10 2023
Tham khảo:
a,
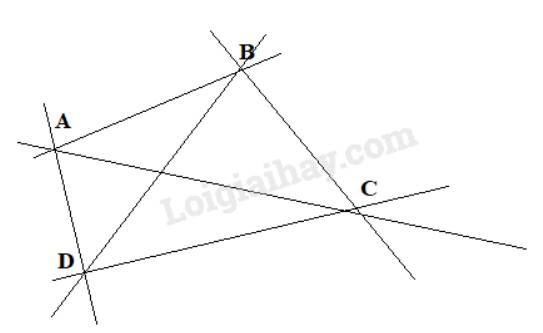
Có 6 đường thẳng đi qua hai trong bốn điểm đã cho. Đó là các đường thẳng: AB, AC, AD, BC, BD, CD.
b,
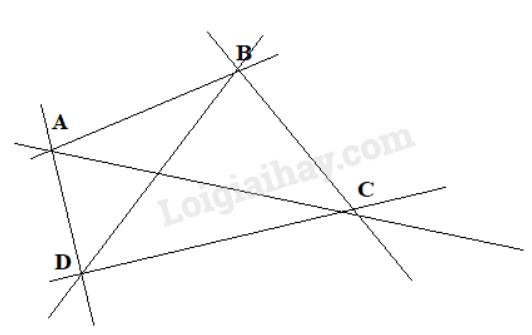
Có 12 tia với gốc là một trong bốn điểm đã cho và đi qua một trong 3 điểm còn lại. Đó là các tia: AB, BA, AC, CA, AD, DA, BC, CB, BD, DB, CD, DC.
c,
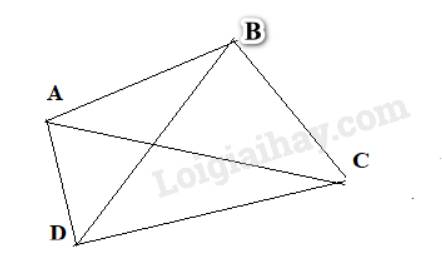
Có 6 đoạn thẳng có hai mút là hai trong bốn điểm đã cho. Đó là các đoạn thẳng: AB,AC,AD,BC,BD,CD.
23 tháng 7 2023
Có \(C^2_4=6\left(đường\right)\) đi qua 2 điểm trong 4 điểm đã cho
CM
10 tháng 6 2019
Bốn điểm A, B, C, D thẳng hàng vì hai điểm C, D đều thuộc đường thẳng AB
NT
7 tháng 10 2016
Từ câu A:B:C thẳng hàng và B:C:D thằng hàng ta suy ra A và D thẳng hàng
Thì A;bB;C;D thẳng hàng