Cho tam giác ABC vuông tại A, AB=6cm, AC=8cm. Phân giác AD. Kẻ DH vuông góc với AB. Tính DH,AD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C 6 D H 8
Vì \(AC\perp AB;HD\perp AB\Rightarrow AC//HD\)
Áp dụng hệ quả Ta lét ta có : \(\frac{BD}{BC}=\frac{HD}{AC}\)(*)
Vì AD là đường phân giác ^A nên : \(\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow\frac{DC}{AC}=\frac{BD}{AB}\)
Lại có : \(BC^2=AB^2+AC^2=36+64=100\Rightarrow BC=10\)cm
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{DC}{AC}=\frac{BD}{AB}=\frac{DC+BD}{AC+AB}=\frac{10}{14}=\frac{5}{7}\)
\(\Rightarrow DC=\frac{5}{7}AC=\frac{5}{7}.8=\frac{40}{7}\)cm ; \(BD=\frac{5}{7}AB=\frac{5}{7}.6=\frac{30}{7}\)cm
Thay vào (*) ta được : \(\frac{\frac{30}{7}}{10}=\frac{HD}{8}\Rightarrow10HD=\frac{240}{7}\Rightarrow HD=\frac{24}{7}\)cm
Có : \(\frac{BH}{AB}=\frac{HD}{AC}\)( hệ quả Ta lét ) \(\Rightarrow BH=\frac{AB.HD}{AC}=\frac{6.\frac{24}{7}}{8}=\frac{18}{7}\)cm
\(\Rightarrow AH=AB-BH=6-\frac{18}{7}=\frac{24}{7}\)cm
Áp dụng định lí Pytago tam giác AHD vuông tại H ta có :
\(AD^2=AH^2+HD^2=\left(\frac{24}{7}\right)^2+\left(\frac{24}{7}\right)^2=2\left(\frac{24}{7}\right)^2\)
\(\Rightarrow AD=\frac{24\sqrt{2}}{7}\)cm o.O bạn check lại xem nhé

xét tam giác ABC vuông tại A có \(BC^2=AB^2+AC^2\left(pytagor\right)\)
\(\Rightarrow BC=10\left(cm\right)\)
xét tam giác ABC ta có AD là đường phân giác => \(\frac{BD}{AB}=\frac{DC}{AC}=\frac{BC}{AB+AC}=\frac{5}{7}\)
=> BD= 30/7 (cm) ; DC= 40/7 (cm)
b/ có DH vuông góc AB ; AC vuông góc AB (tam giác vuông)
=> DH//AC => \(\frac{DH}{AC}=\frac{BD}{BC}=\frac{BH}{AB}\)(hệ quả Thales) => \(DH=\frac{AC.BD}{BC}=\frac{24}{7}\left(cm\right)\)
ta có HAD=CAD (p/giác) ; HDA=CAD( 2 góc slt; DH//AC) => HAD=HDA => tam giác AHD cân tại H
mà tam giác AHD vuông tại H => tam giác AHD vuông cân tại H
=> \(AD^2=2DH^2\)=> \(AD=\frac{24\sqrt{2}}{7}\left(cm\right)\)
mình ko tính ra số thập phân. Bạn tự tính nhé. Chúc bn học tốt

D C H B A
Mình nói tóm tắt thôi nhé!
a) chứng minh được tam giác ABD = tam giác HBD (cạnh huyền - góc nhọn) => AD = DH (2 cạnh tương ứng)
b) tam giác HDC vuông tại H nên DC là cạnh lớn nhất => DC > DH; mà DH = AH (c/m trên) => DC > AD
c) Mình chưa nghĩ ra![]()
Câu c là tính HC nhé bạn!
c) Tính BC bằng cách dùng định lí pytago trong tam giác ABC, ta có: BC = 10cm
BH + HC = BC = 10cm
BH = AB = 6cm
=> HC = 10 - 6 = 4 cm
Chúc bạn học tốt!![]()

A B C 6 10 D H K
a, Xét \(\Delta ABC\)VUÔNG tại A
Áp dụng định lý pitago ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\)
\(\Rightarrow AB^2=10^2-6^2\)
\(\Rightarrow AB^2=100-36\)
\(\Rightarrow AB^2=64\)
\(\Rightarrow AB=\sqrt{64}=8\)
VẬY AB=8 cm
b, Xét \(\Delta ABD\)và \(\Delta HBD\)CÓ:
\(\widehat{BAD}=\widehat{BHD}=90độ\)
\(\widehat{ABD}=\widehat{HBD}\)(do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta HBD\)(ch-gn)
\(\Rightarrow AD=HD\)(2 CẠNH TƯƠNG ỨNG)
c,Do \(\Delta ABD=\Delta HBD\left(câub\right)\)
\(\Rightarrow\widehat{BDA}=\widehat{BDH}\)(2 góc tương ứng)
lại có \(\widehat{ADK}=\widehat{HDC}\)(đối đỉnh)
\(\Rightarrow\widehat{BDA}+\widehat{ADK}=\widehat{BDH}+\widehat{HDC}\)
\(\Rightarrow\widehat{BDK}=\widehat{BDC}\)
Xét \(\Delta KBD\) VÀ \(\Delta CBD\)CÓ:
\(\widehat{ABD}=\widehat{CBD}\)(Do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\widehat{BDK}=\widehat{BDC}\left(cmt\right)\)
Do đó \(\Delta KBD=\Delta CBD\left(g-c-g\right)\)
\(\Rightarrow BK=BC\)(2 CẠNH TƯƠNG ỨNG)
\(\Rightarrow\Delta KBC\) cân tại B

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=BC^2-AB^2=13^2-12^2=169-144=25\)
=>\(AC=\sqrt{25}=5\left(cm\right)\)
b: XétΔBAC có BD là phân giác
nên \(\dfrac{AD}{BA}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{12}=\dfrac{CD}{13}\)
D nằm giữa A và C
=>AD+DC=AC
=>AD+DC=5(cm)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{12}=\dfrac{CD}{13}=\dfrac{AD+CD}{12+13}=\dfrac{5}{25}=0,2\)
=>\(AD=2\cdot12=2,4\left(cm\right);CD=2\cdot13=2,6\left(cm\right)\)
c: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
=>DA=DH
mà DA=2,4(cm)
nên DH=2,4(cm)

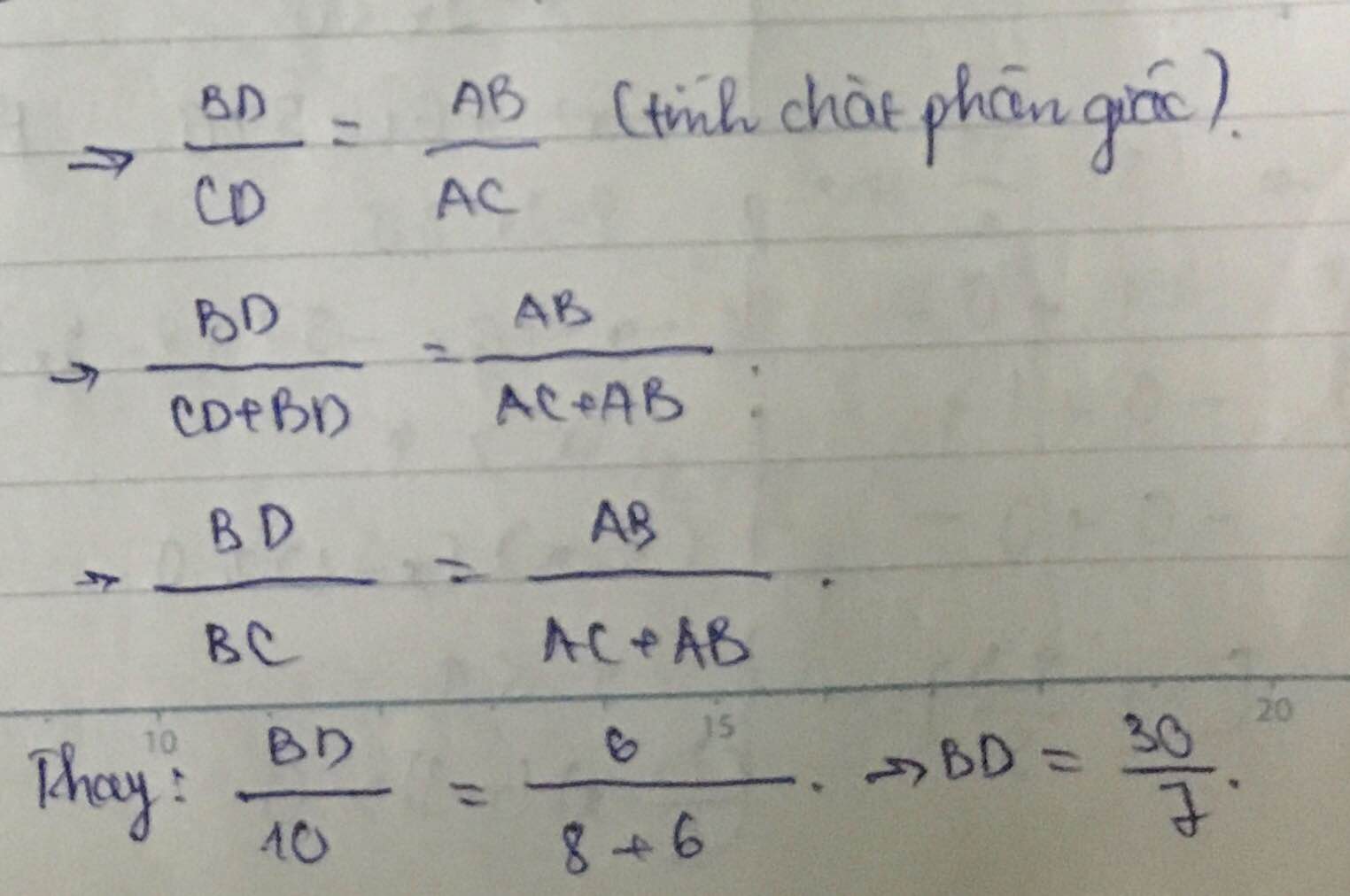
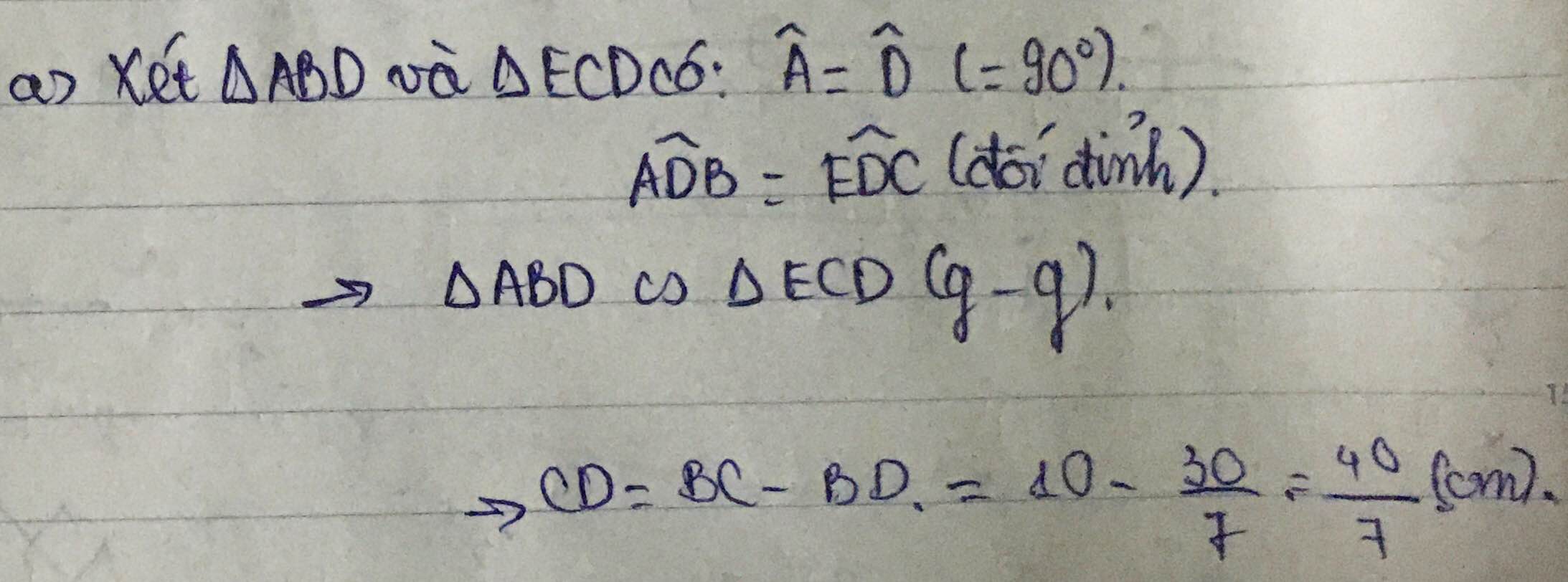
Áp dụng Pitago ta có : BC = 10
Áp dụng tính chất của tia phân giác ta có : BD/DC = AB/AC = 3/4
=> BD/BC = 3/7 => BD = 30/7 cm, CD = 40/7 cm
HD // AC => HD / AC = BD / BC
=> HD = 30/70.8 = 24/7
Do góc HAD = 45 độ => T/g HAD vuông cân => AD^2 = 1152/49 => AD = \(\frac{24\sqrt{2}}{7}\)cm