Bài 1 : tìm GTLN của A = ( 1-xn) x (1+xn) + ( 2-yn) x ( 2+yn) ( Với n thuộc N* )
Bài 2 : Tìm x biết : x3 + 3x2 + 3x + 1 = -1
Bài 3 : Chứng tỏ rằng :
a ) A = 20053 - 1 chia hết 2004
b ) B = 20003+125 chia hết 2010
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ta có: \(x\left(x-y\right)+y\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y\right)\)
\(=x^2-y^2\)
b: Ta có: \(x^{n-1}\left(x+y\right)-y\left(x^{n-1}+y^{n-1}\right)\)
\(=x^n+x^{n-1}\cdot y-x^{n-1}\cdot y-y^n\)
\(=x^n-y^n\)

Chọn A.
Ta có: 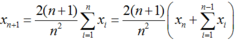
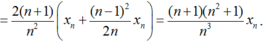
Do đó: 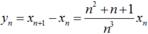
- Ta chứng minh dãy (yn) tăng.
Ta có: 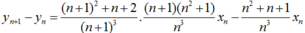
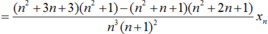
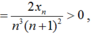
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
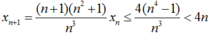
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: 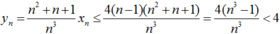
Vậy bài toán được chứng minh.

bài 1:
a 2x(x-5)-2x^2=20
<=>2x^2-10x-2x^2=20
<=>-10x=20
<=>x=-2
v....
b x^2-2x+1=0
<=>(x-1)^2=0
<=>x-1=0
<=>x=1
v...
bài 3
A=x-x^2+1=-(x^2-x-1)=-(x^2-2*x*1/2+1/4-5/4)=-(x-1/2)^2+5/4<=5/4
dấu bằng xảy ra <=>x=1/2
bài 2 mình ko biết làm sorry cậu

Bài 1: Ta có 200920 = (20092)10 = (2009.2009)10
2009200910 = (10001.2009)10
Mà 2009 < 10001 ➩ (2009.2009)10 < (10001.2009)10
Vậy 200920 < 2009200910



xn - 1(x + y) - y(xn - 1 + yn - 1)
= xn - x + y - yxn - y2 n - 1
1/\(A=\left(1-x^n\right)\left(1+x^n\right)+\left(2-y^n\right)\left(2+y^n\right)\)
\(=1-x^{2n}+4-y^{2n}=5-x^{2n}-y^{2n}\)
Vì \(x^{2n}\ge0;y^{2n}\ge0\Rightarrow x^{2n}+y^{2n}\ge0\Rightarrow-\left(x^{2n}+y^{2n}\right)\le0\)
\(\Rightarrow A=5-\left(x^{2n}+y^{2n}\right)=5-x^{2n}-y^{2n}\le5\)
Dấu "=" xảy ra khi x = y = 0
Vậy Amax = 5 khi x = y = 0
2/
x3+3x2+3x+1=-1
<=>(x+1)3=-1
<=>x+1=-1
<=>x=-2
3/
a, \(A=2005^3-1=\left(2005-1\right)\left(2005^2-2005.1+1^2\right)=2004\left(2005^2-2005+1\right)⋮2004\)
b, \(B=2000^3+125=2000^3+5^3=\left(2000+5\right)\left(2000^2-2000.1+1^2\right)=2010\left(\frac{2000^2}{2}-\frac{2000}{2}+\frac{1}{2}\right)⋮2010\)