Cho tam giác ABC có AB = 48cm, BC = 50cm, AC = 14cm. Tính độ dài phân giác giác góc C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔCBA có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{30}=\dfrac{CD}{40}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=50
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{50}{7}\)
=>\(BD=\dfrac{150}{7}\left(cm\right);CD=\dfrac{200}{7}\left(cm\right)\)
Xét ΔABC có DE//AB
nên \(\dfrac{DE}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{DE}{30}=\dfrac{200}{7}:50=\dfrac{4}{7}\)
=>\(DE=\dfrac{120}{7}\left(cm\right)\)
b: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
=>Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot30\cdot40=15\cdot40=600\left(cm^2\right)\)

a) Xét tam giác BAD và CAD có:
AB=AC=14cm
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác)
AD cạnh chung
=> \(\Delta BAD=\Delta CAD\left(c.g.c\right)\)
=> BD=CD
Mà BD+CD=BC=12 cm
=> BD=DC=12:2=6(cm)
b) Vì AB=AC, BD=DC
=> AD là đường trung trực của BC
=> AD _|_ BC
=> \(S_{\Delta ABD}=\frac{1}{2}AD\cdot BD;S_{\Delta CAD}=\frac{1}{2}AD\cdot DC\)
\(\frac{S_{\Delta ABD}}{S_{\Delta CAD}}=\frac{AD\cdot BD}{AD\cdot DC}=\frac{AD}{DC}=1\)

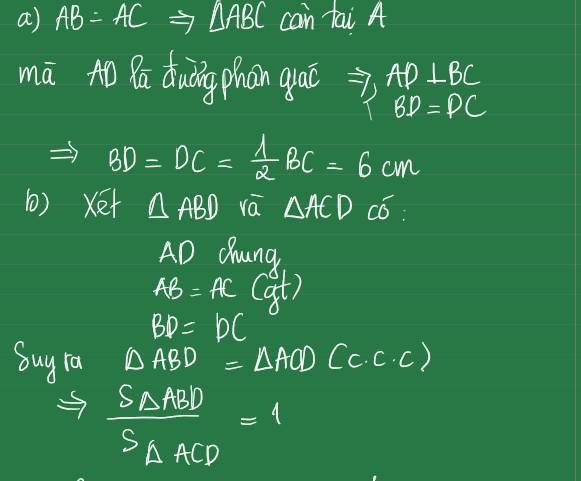
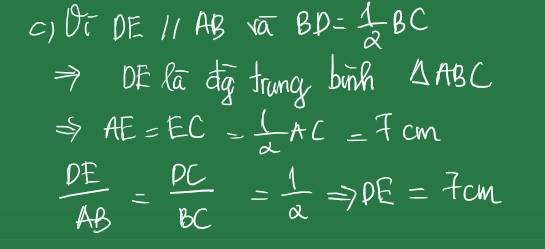
C A B 14cm 48cm 50cm
Xét tam giác ABC, ta có
BC2 = 502 = 2500
AB2 + AC2 = 142 + 482 = 2500
=> BC2 = AB2 + AC2
=> Tam giác ABC vuông tại A
Có DA/DB = CA/CB = 14/50 = 7/25 (tính chất tia phân giác)
=> DB = 25/7 DA.
Ta có DA + DB = AB
⇔ DA + 25/7 DA = AB ⇔ DA. 32/7 = 48 ⇔ DA = 10,5cm
Xét tam giác vuông ACD, theo đinh lí Pi-ta-go ta có:
CD2 = AC2 + AD2 = 142 + 10,52 = 306,25 => CD = 17,5cm