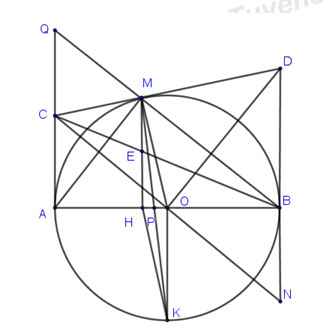
Cho hình thang ABCD ,góc A ,D vuông .M thuộc AB.Qua M kẻ đường thẳng vuông góc với MD cắt BC tại N.chứng minh MD=Mn và biết DC=2AB=2AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
28 tháng 9 2018
Con tham khảo tại câu dưới đây nhé.
Câu hỏi của Huyen Nguyen - Toán lớp 8 - Học toán với OnlineMath
29 tháng 5 2022
xét đường tròn \(\left(O\right)\) có \(MD\) và \(BD\) là tiếp tuyến với \(B;D\) , là tiếp điểm
\(\Rightarrow MD=DB\) ( tính chất tiếp tuyến )
xét tam giác \(MOD\) và tam giác \(BOD\) , có :
\(MD=BD\) ( cmt )
\(MO=OB\) ( cùng là bán kính đường tròn )
\(OD\) chung
\(\Rightarrow\Delta MOD=\Delta BOD\Rightarrow\) ∠ \(MDO\) \(=\) ∠ \(BDO\Rightarrow OD\) là phân giác ∠\(MDB\)
xét tam giác \(CDN\) có :
\(OD\) là đường cao ( do \(OD\perp CN\) )
\(OD\) là phân giác ∠ \(MDB\)
suy ra : tam giác \(CDN\) cân tại \(D\) , suy ra \(CD=ND\) ( đpcm )
11 tháng 7 2018
Từ M kẻ đường thẳng vuông góc với AD cắt BD tại I. Hạ DH vuông góc BC tại H
Ta có: AB vuông góc AD; MI vuông góc AD => AB // MI => ^MIB = 1800 - ^ABD
Xét \(\Delta\)ADB: ^BAD = 900; AB=AD => \(\Delta\)ADB vuông cân tại A => ^ABD = 450
=> ^MIB = 1350 (1)
Dễ thấy tứ giác ADHB là hình vuông => DH=BH=AB=1/2BC => DH=BH=CH = 1/2BC
=> \(\Delta\)BDC vuông tại D => ^BDC = 900 => ^MDN = ^BDC + ^ADB = 900 + 450 = 1350 (2)
(1) + (2) => ^MIB = ^MDN
Xét \(\Delta\)MIB & \(\Delta\)MDN: ^MIB = ^MDN; IM=DM (Dễ c/m); ^IMB = ^DMN (Cùng phụ ^IMN)
=> \(\Delta\)MIB = \(\Delta\)MDN (g.c.g) => MB=MN (đpcm).