Cho 3x-y=3z và 2x+y=7z. Tính giá trị biểu thức \(M=\frac{x^2-2xy}{x^2+y^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
1
25 tháng 6 2018
\(3x-y=3z\Rightarrow-y=3z-3x\Rightarrow y=3x-3z\)
\(2x+y=7z\Rightarrow y=7z-2x\)\(\Rightarrow3x-3z=7z-2x=y\Rightarrow3x-3z-7z+2x=5x-10z=0\Rightarrow x-2z=0\Rightarrow x=2z\)
\(2x+y=7z\Rightarrow2\cdot2z+y=7z\Rightarrow4z+y=7z\Rightarrow y=3z\)
\(M=\frac{x^2-2xy}{x^2+y^2}=\frac{\left(2z\right)^2-2\cdot2z\cdot3z}{\left(2z\right)^2+\left(3z\right)^2}=\frac{4z^2-12z^2}{4z^2+9z^2}=-\frac{8z^2}{13z^2}=-\frac{8}{13}\)
16 tháng 12 2020
Ta có: \(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Leftrightarrow3x-y+2x+y=10z\)
\(\Leftrightarrow5x=10z\)
hay x=2z
Thay x=2z vào biểu thức 3x-y=3z, ta được:
\(3\cdot2z-y=3z\)
\(\Leftrightarrow6z-y=3z\)
hay y=3z
Thay x=2z và y=3z vào biểu thức \(M=\dfrac{x^2-2xy}{x^2+y^2}\), ta được:
\(M=\dfrac{\left(2z\right)^2-2\cdot2z\cdot3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{13z^2}=\dfrac{-8z^2}{13z^2}=\dfrac{-8}{13}\)
Vậy: \(M=\dfrac{-8}{13}\)
TG
16 tháng 12 2020
\(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5x=10z\\3x-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\3.2z-y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2z\\y=3.2z-3z=6z-3z=3z\end{matrix}\right.\)
Có: \(M=\dfrac{x^2-2xy}{x^2+y^2}=\dfrac{\left(2z\right)^2-2.2z.3z}{\left(2z\right)^2+\left(3z\right)^2}=\dfrac{4z^2-12z^2}{4z^2+9z^2}=\dfrac{-8z^2}{13z^2}==-\dfrac{8}{13}\)
NN
3
23 tháng 11 2016
Mình sửa lại đề cho đúng nhé
\(\hept{\begin{cases}3x-y=3z\\2x+y=7z\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2z\\y=3z\end{cases}}\)
Thế vô M ta được
23 tháng 11 2016
\(M=\frac{x^2-2xy}{x^2+y^2}=\frac{4z^2-2.2z.3z}{4z^2+9z^2}=-\frac{8}{13}\)
2 tháng 12 2017
Ta có:
\(\left\{{}\begin{matrix}3x-y=3z\\2x+y=7z\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}5x=10z\\2x+y=7z\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}x=2z\\y=3z\end{matrix}\right.\)
Thay x = 2z và y = 3z vào biểu thức M ta được:
M = \(\dfrac{\left(2z\right)^2-2.2z.3z}{\left(2z\right)^2+\left(3z\right)^2}\)
= \(\dfrac{4z^2-12z^2}{4z^2+9z^2}\)
= \(\dfrac{-8z^2}{13z^2}\)
= \(\dfrac{-8}{13}\)
Vậy...
PT
1
CM
27 tháng 2 2017
Từ 3x – y = 3z và 2x + y = 7z ⇒ x = 2z; y = 3z. Thay vào M ta được
NM
Nguyễn Minh Quang
Giáo viên
26 tháng 1 2021
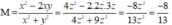
ta có hệ
\(\hept{\begin{cases}3x-y=3z\\2x+y=7z\end{cases}}\)cộng hai phương trình lại , ta có \(5x=10z\Rightarrow x=2z\Rightarrow y=3z\) thế vào M ta có
\(M=\frac{4z^2-2.2z.3z}{4z^2+9z^2}=\frac{4-12}{4+9}=-\frac{8}{13}\)
ta có 5x=10z=> x=2z=> y=3z
Tháy vào, ta có \(M=\frac{4z^2-12z^2}{4z^2+9z^2}=\frac{-8z^2}{13z^2}=-\frac{8}{13}\)
Ta có:
\(3x-y+2x+y=3z+7z\)
\(5x=10z\)
\(x=2z\)
thay:\(4z+y=7z\) \(\Rightarrow y=3z\)
Thay vào M ta đc:M=\(\frac{4z^2-12z^2}{4z^2+9z^2}\) =\(\frac{-8z^2}{13z^2}=\frac{-8}{13}\)
vậy\(M=\frac{-8}{13}\) nếu\(3x-y=3z;2x+y=7z\)