Cho ABCD hình thang cân. Đường thẳng AD;BC cắt tại M, AC và BD cắt tại O. Chứng minh: MO vuông góc AB
giải giúp mình plz
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
=>ΔABC=ΔBAD
=>góc OBA=góc OAB
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
b: Xét ΔEDC có AB//DC
nên EA/AD=EB/BC
mà AD=BC
nên EA=EB
EA+AD=ED
EB+BC=EC
mà EA=EB và AD=BC
nên ED=EC
EA=EB
OA=OB
=>EO là trung trực của AB
EC=ED
OC=OD
=>EO là trung trực của CD

a) i) \(ABCD\) là hình thang cân (gt)
\( \Rightarrow \widehat A = \widehat B\) (1) và \(DC\) // \(AE\)
Vì \(AD\;{\rm{//}}\;CE\) (gt)
\(\widehat A = \widehat {CEB}\) (cặp góc đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {CEB} = \widehat B\)
Suy ra \(\Delta CEB\) là tam giác cân.
ii) \(\Delta CEB\) cân tại \(C\) (cmt)
Suy ra: \(CE = BC\) (3)
Xét \(\Delta ADE\) và \(\Delta CED\) ta có:
\(\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}\) (\(AD\)// \(CE\), cặp góc so le trong)
\(DE\) chung
\(\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}\) (\(CD\) // \(AB\), cặp góc so le trong)
Suy ra: \(\Delta ADE = \Delta CED\) (g-c-g)
Suy ra: \(AD = CE\) (4)
Từ (3) và (4) suy ra: \(AD = BC\)
b) Chứng minh tương tự như ý a) ta có: Hình thang cân \(MNPQ\) có hai cạnh bên \(MQ = NP\)
Xét tam giác \(\Delta MQP\) và \(\Delta NPQ\) ta có:
\(MQ = NP\) (cmt)
\(\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}\) (do \(MNPQ\) là hình thang cân)
\(PQ\) chung
Suy ra: \(\Delta MQP = \Delta NPQ\) (c-g-c)
\( \Rightarrow MP = NQ\) (hai cạnh tương ứng)

Gọi H là giao điểm của AC và BD
Vì AF//BC
Áp dụng hệ quả Talet :
=> HF/HB = AH/HC
Ta có : HE//HA = HB/HD
Mà AB//CD
=> HB/HA = HA/HC
=> HE /HA = HF/HB
=> EF//AB
=> EDCF là hình thang
Vì ABCD là hình thang cân
=> ADC = BCD
AD = BC
Xét ∆ACD và ∆BDC ta có :
DC chung
AD = BC
ADC = BCD
=> ∆ACD = ∆BDC (c.g.c)
=> BDC = ACD
=> EDCF là hình thang cân (dpcm)
b) Kéo dài EF sao cho lần lượt cắt AD tại G và BC tại O
Vì EF//DC (cmt)
=> GO//DC
Mà DC//AB
=> AB//GO//DC
=> GO là đường trung bình hình thang ABCD
=> GO = \(\frac{5\:+\:10}{2}=\:7,5\)cm
Mà GO là đường trung bình hình thang
=> G là trung điểm AD ; O là trung điểm BC
Vì GO//AB
=> GE//AB
Mà G là trung điểm AD
=> GE là đường trung bình ∆ABD
=> GE = \(\frac{5}{2}\)= 3,5 cm
Vì GO //AB
=> FO//AB
Mà O là trung điểm BC
=> FO là đường trung bình ∆ABC
=> FO = \(\frac{5}{2}=\:3,5\)cm
=> EF = 7,5 - 3,5 - 3,5 = 0,5cm

a ) Xét Δ∆ADC và Δ∆BCD, ta có:
AD = BC (tính chất hình thang cân)
∠∠(ADC) = ∠∠(BCD) (gt)
DC chung
Do đó: Δ∆ADC = Δ∆BCD (c.g.c) ⇒ ∠C1∠�1= ∠D1∠�1
Trong Δ∆OCD ta có: ∠C1∠�1= ∠D1∠�1 ⇒ Δ∆OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
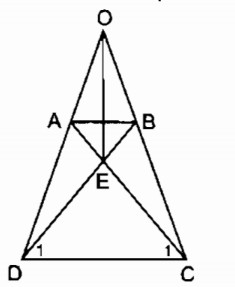
ADC=ˆBCD(gt)⇒ˆODC=ˆOCD���^=���^(��)⇒���^=���^
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
⇒ˆD1=ˆC1⇒�^1=�^1
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
E≢ O. Vậy OE là đường trung trực của AB.

Đáp án cần chọn là: C
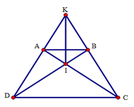
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra A C D ^ = B D C ^ (hai góc tương ứng), suy ra tam giác ICD cân tại I.
Nên C sai vì ta chưa đủ điều kiện để IC = CD
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K nên B đúng.
Xét tam giác KDI và tam giác KCI có:
+ KD = KC (do ΔKCD cân tại K))
+ KI là cạnh chung
+ IC = ID
Suy ra ΔKDI = ΔKCI (c.c.c)
Suy ra K D I ^ = C K I ^ , do đó KI là phân giác A K B ^ nên D đúng.
Ta có AB // CD (do ABCD là hình thang) nên K A B ^ = K C D ^ ; K B A ^ = K C D ^ (các cặp góc đồng vị bằng nhau)
Mà K D C ^ = K C D ^ (tính chất hình thang cân) nên K A B ^ = K C D ^ (tính chất hình thang cân) nên hay ΔKAB cân tại K. Do đó A đúng
xét tam giác MDC có góc D lớn và góc C lớn = => tam giác MDC cân tại M
cm tam giác ODC cân tại o
xét 2 tam giác MOD và tam giác MOC = (c.c.c)
=> mo là phân giác
mà trong tam giác cân, phân giác là đg cao
=> mo vuông góc vs AB