Trên ( O;R ) cho trước , vẽ dây cung AB cố định không đi qua O. Điểm M bất kỳ trên tia BA sao cho M nằm ngoài đường tòn ( O; R) . Từ M kẻ hai tiếp tuyến MC và MD với đường tròn ( O; R) ( C và D là hai tiếp điểm)
a) C/m OCMD là tứ giác nội tiếp
b) C/m MC2=MA.MB
c) Gọi H là trung điểm đoạn AB , F là giao điểm của CD và OH
C/m F là điểm cố định khi M thay đổi


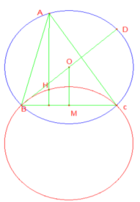
c) OM cắt CD tại F
Ta có OK.OM=OC2=R2OK.OM=OC2=R2
ΔOHM∼ΔOKF⇒OHOK=OMOFΔOHM∼ΔOKF⇒OHOK=OMOF
⇒OF=OK.OMOH=R2OH⇒OF=OK.OMOH=R2OH (không đổi)
mà OF nằm trên đường cố định nên F là điểm cố định khi M thay đổ
c)OM cắt CD tại F
Ta có \(OK.OM=OC^2=R^2\)
\(\Delta OHM~\Delta OKF\Rightarrow\frac{OH}{OK}=\frac{OM}{OF}\)
\(OF=\frac{OK.OM}{OH}=\frac{R^2}{OH}\)( không đổi)
mà OF nằm trên đường cố định nên F là điểm cố định khi M thay đổi