Viết các biểu thức sau dưới dạng tổng
a) (a2+2a+3)(a2+2a-3)
b) (a2+2a+3)(a2-2a-3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 7 2023
a,hđt số 3 = \(\left(a^2+2a\right)^2-9\)
b,hđt số 3=\(\left[x-\left(y-6\right)\right]\left[x+\left(y-6\right)\right]\)(đổi dấu làm ngoặc khi trước nó là dấu trừ)=\(x^2-\left(y-6\right)^2\)
19 tháng 7 2023
a) \(\left(a^2+2a+3\right)\left(a^2+2a-3\right)\)
\(=\left(a^2+2a\right)^2+3.\left(-3\right)\)
\(=\left(a^2+2a\right)^2-9\)
b) \(\left(x-y+6\right)\left(x+y-6\right)\)
\(=\left[x-\left(y-6\right)\right]\left[x+\left(y-6\right)\right]\)
\(=x^2-\left(y-6\right)^2\)
PA
0
A
1
13 tháng 5 2022
Ta có \(A\left(1\right)=B\left(-2\right)\Leftrightarrow12+2a+a^2=8-\left|2a+3\right|\left(-2\right)+a^2\)
\(\Leftrightarrow4+2a=2\left|2a+3\right|\)
đk a >= -2
\(\left[{}\begin{matrix}4a+6=4+2a\\4a+6=-2a-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=-1\left(tm\right)\\a=-\dfrac{5}{3}\left(ktm\right)\end{matrix}\right.\)
CM
23 tháng 10 2018
Ta có 
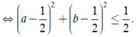
Ta có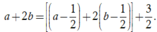 
Áp dụng bất đẳng thức Bunhiacopxky, ta có
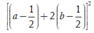
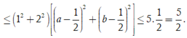
Do đó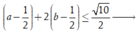 
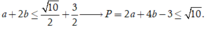
Dấu "x" xảy ra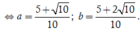 
Chọn C.
Ta thấy (1) là hình tròn tâm 
Ta có 
Xem đây là phương trình đường thẳng.
Để đường thẳng và hình tròn có điểm chung 
HQ
Hà Quang Minh
Giáo viên
20 tháng 8 2023
\(a,\left(2a-3\right)\left(a+1\right)+\left(a^2+6a+9\right):\left(a+3\right)\\ =2a^2-a-3+\left(a+3\right)^2:\left(a+3\right)\\ =2a^2-a-3+a+3\\ =2a^2\\ b,\left(3x-5y\right)\left(-xy\right)^2-3x^2y^2+4x^2y^3\\ =3x^3y^2-5x^2y^3-3x^2y^2+4x^2y^3\\ =3x^3y^2-3x^2y^2-x^2y^3\\ c,x\left(x-2\right)^2-\left(x+2\right)\left(x^2-2x+4\right)+4x^2\\ =x^3-4x^2+4x-x^3-8+4x^2\\ =4x-8\)
24 tháng 8 2021
c: Ta có: \(a\left(a+2b\right)^3-b\left(2a+b\right)^3\)
\(=a^4+6a^3b+12a^2b^2+8ab^3-8a^3b-12a^2b^2-6ab^3-b^4\)
\(=a^4-2a^3b+2ab^3-b^4\)
\(=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)-2ab\left(a^2-b^2\right)\)
\(=\left(a-b\right)^3\cdot\left(a+b\right)\)
a) Áp dụng hằng đẳng thức : \(a^2-b^2+\left(a-b\right)\left(a+b\right)\)
Ta có ; \(\left(a^2+2a+3\right)\left(a^2+2a-3\right)\)
\(=\left[\left(a^2+2a\right)+3\right]\left[\left(a^2+2a\right)-3\right]\)
\(=\left(a^2+2a\right)^2-3^2\)
\(=\left(a^2+2a\right)^2-9\)