Cho x,y là hai số dương thoả mãn x \(\ge\)xy+1. Tìm giá trị lớn nhất của P = \(\frac{xy}{x^2+y^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
22 tháng 2 2020
\(x+y=1\Rightarrow2\sqrt{xy}\le1\Rightarrow\sqrt{xy}\le\frac{1}{2}\)
\(\Rightarrow xy\le\frac{1}{4}\Rightarrow\frac{1}{xy}\ge4\)
Áp dụng bđt cauchy cho 3 số dương:
\(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{xy}\ge3\sqrt[3]{\frac{1}{x^2}.\frac{1}{y^2}.\frac{1}{xy}}=3.\frac{1}{xy}\ge3.4=12\)
Dấu "=" xảy ra khi \(x=y=\frac{1}{2}\)
TN
Cho các số thực dương x,y thoả mãn xy+x+y\(\ge\)8. Tìm giá trị nhỏ nhất của biểu thức P= \(x^2+y^2\)
3
T
21 tháng 8 2019
Ta có: \(8\le xy+x+y\le\frac{\left(x+y\right)^2}{4}+x+y\)
Từ đó suy ra \(a+b\ge4\Rightarrow16\le\left(a+b\right)^2\le2\left(a^2+b^2\right)=2P\Rightarrow P\ge8\)
Vậy..
P/s: chắc là vậy đó!
15 tháng 5 2018
\(\frac{1}{2}=\frac{1}{x^2}+\frac{1}{y^2}\ge\frac{2}{xy}\)
\(\Leftrightarrow xy\ge4\)
\(\Rightarrow A=xy+2017\ge4+2017=2021\)
25 tháng 2 2021
Ta có: \(\frac{xy+1}{x+y}\ge\frac{3y+1}{x+y}\ge\frac{3y+1}{2y}>\frac{3y}{2y}=\frac{3}{2}\)( mâu thuẫn với gt)
giả sử \(a\le2\Rightarrow a\in\left\{1;2\right\}\)
+ Với a=1 \(\Rightarrow M=\frac{y^3+1}{y^3+1}=1\)
+ Với a=2 \(\Rightarrow M=\frac{8y^3+1}{y^3+8}\)
Từ đk \(\frac{xy+1}{x+y}=\frac{2y+1}{y+2}< \frac{3}{2}\Rightarrow b< 4\)
=> \(b\in\left\{1;2;3\right\}\)
+ Với b=1 \(\Rightarrow M=\frac{9}{9}=1\)
+ Với b=2 \(\Rightarrow M=\frac{8.8+1}{8+8}=\frac{65}{16}\)
+ vỚI b=3 \(\Rightarrow M=\frac{8.27+1}{27+8}=\frac{217}{35}\Leftrightarrow\hept{\begin{cases}a=2\\b=3\end{cases}}\) hoặc ngược lại.
30 tháng 9 2018
\(P\le\frac{x}{2\sqrt{x^4.y^2}}+\frac{y}{2\sqrt{x^2.y^4}}=\frac{x}{2x^2y}+\frac{y}{2xy^2}=\frac{1}{2xy}+\frac{1}{2xy}=\frac{1}{xy}=1\)
Dấu "=" xảy ra khi x=y=1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
\(x\ge xy+1\Rightarrow1\ge y+\dfrac{1}{x}\ge2\sqrt{\dfrac{y}{x}}\Rightarrow\dfrac{y}{x}\le\dfrac{1}{4}\)
\(Q^2=\dfrac{x^2+2xy+y^2}{3x^2-xy+y^2}=\dfrac{\left(\dfrac{y}{x}\right)^2+2\left(\dfrac{y}{x}\right)+1}{\left(\dfrac{y}{x}\right)^2-\dfrac{y}{x}+3}\)
Đặt \(\dfrac{y}{x}=t\le\dfrac{1}{4}\)
\(Q^2=\dfrac{t^2+2t+1}{t^2-t+3}=\dfrac{t^2+2t+1}{t^2-t+3}-\dfrac{5}{9}+\dfrac{5}{9}\)
\(Q^2=\dfrac{\left(4t-1\right)\left(t+6\right)}{9\left(t^2-t+3\right)}+\dfrac{5}{9}\le\dfrac{5}{9}\)
\(\Rightarrow Q_{max}=\dfrac{\sqrt{5}}{3}\) khi \(t=\dfrac{1}{4}\) hay \(\left(x;y\right)=\left(2;\dfrac{1}{2}\right)\)
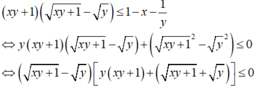
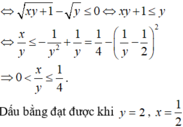
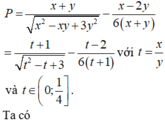
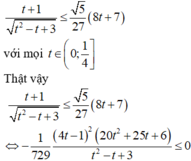
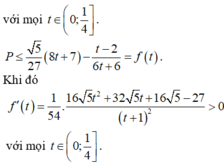
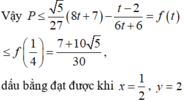
Bài này có nhiều cách làm nhá cái này mình làm bạn tham khảo thôi nhá
Ta có \(P=\frac{xy}{x^2+y^2}\)
\(\Rightarrow\frac{1}{P}=\frac{x^2+y^2}{xy}\)
Mà Theo BĐT Cô si thì
\(x^2+y^2\ge2xy\)
\(\Rightarrow\frac{1}{P}\ge\frac{2xy}{xy}=2\)
\(\frac{1}{P}\ge2\Leftrightarrow2P\le1\Leftrightarrow P\le\frac{1}{2}\)
Vậy Max \(P=\frac{1}{2}\) Khi x=y=...
Có cách ngắn hơn nhưng minhf lười =))
Vậy khi x=y= gì ạ