Chứng minh:
a) Với mọi x,y bất kỳ ,2+x²+y²≥(x+y)×2
b) (m+1)²≥4m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(x^2+y^2-2x+4y+6=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1>0\forall x,y\)
b) \(2x^2+2x+3=2\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{5}{2}\)
\(=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{5}{2}\ge\dfrac{5}{2}>0\forall x\)
c) \(x^2+y^2+z^2\ge xy+yz+xz\)
\(\Leftrightarrow2x^2+2y^2+2z^2\ge2xy+2yz+2xz\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(y^2+2yz+z^2\right)+\left(x^2+2xz+z^2\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(x-z\right)^2\ge0\left(đúng\right)\)
\(ĐTXR\Leftrightarrow x=y=z\)

⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
x^2+4y^2+z^2-2x-6z+8y+15
=x^2+4y^2+z^2-2x-6z+8y+1+1+4+9
=(x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)+1
=(x-1)^2+4(y+1)^2+(z-3^)2+1
Ta thấy:(x−1)^2≥0
4(y+1)^2≥0
(z−3)^ 2≥0
{(x−1)^24(y+1)^2(z−3)^2≥0
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
⇒(x−1)2+4(y+1)2+(z−3)2+1≥0+1=1>0

Bài 1:
Sửa đề: CMR \(x^3+y^3\ge x^2y+xy^2\)
Xét hiệu:
\(x^3+y^3-(x^2y+xy^2)=(x^3-x^2y)-(xy^2-y^3)\)
\(=x^2(x-y)-y^2(x-y)\)
\(=(x^2-y^2)(x-y)=(x+y)(x-y)(x-y)=(x+y)(x-y)^2\)
Vì \(x+y\geq 0, (x-y)^2\geq 0\) với mọi $x,y$ không âm
\(\Rightarrow x^3+y^3-(x^2y+xy^2)=(x-y)^2(x+y)\geq 0\)
\(\Leftrightarrow x^3+y^3\geq x^2y+xy^2\)
Ta có đpcm.
Bài 2:
$111(x-2)$ không nhỏ hơn $1998$, nghĩa là:
\(111(x-2)\geq 1998\)
\(\Leftrightarrow x-2\geq \frac{1998}{111}=18\)
\(\Leftrightarrow x\geq 20\)
Vậy với mọi giá trị $x\in\mathbb{R}$, $x\geq 20$ thì ta có điều cần thỏa mãn.

Do vai trò của x;y;z là hoàn toàn như nhau, ko mất tính tổng quát, giả sử \(x\ge y\ge z\)
Khi đó 3 số được viết lại: \(\left(x-y\right)^2;\left(y-z\right)^2;\left(x-z\right)^2\)
\(x\ge y\ge z\Rightarrow\left\{{}\begin{matrix}x-y\ge0\\y-z\ge0\\x-z\ge0\end{matrix}\right.\) mà \(x-z=x-y+y-z\Rightarrow\left\{{}\begin{matrix}x-z\ge x-y\\x-z\ge y-z\end{matrix}\right.\)
Đặt \(\sqrt{m}=min\left\{x-y;y-z\right\}\Rightarrow\left\{{}\begin{matrix}x-y\ge\sqrt{m}\\y-z\ge\sqrt{m}\end{matrix}\right.\)
\(\Rightarrow x-z=x-y+y-z\ge2\sqrt{m}\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-y\right)^2\ge m\\\left(y-z\right)^2\ge m\\\left(x-z\right)^2\ge4m\end{matrix}\right.\) \(\Rightarrow6m\le\left(x-y\right)^2+\left(y-z\right)^2+\left(x-z\right)^2\)
\(\Leftrightarrow6m\le2\left(x^2+y^2+z^2\right)-2\left(xy+yz+zx\right)\)
\(\Leftrightarrow6m\le2\left(x^2+y^2+z^2\right)-\left[\left(x+y+z\right)^2-\left(x^2+y^2+z^2\right)\right]\)
\(\Leftrightarrow6m\le3\left(x^2+y^2+z^2\right)-\left(x+y+z\right)^2\le3\left(x^2+y^2+z^2\right)\)
\(\Rightarrow m\le\frac{1}{2}\left(x^2+y^2+z^2\right)\)

Có ![]()
![]()
Đặt t=f(x)+m bất phương trình trở thành: ![]()
![]()
Vậy ![]()
![]()
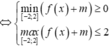
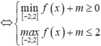
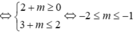
Chọn đáp án B.

Dễ thấy:
\(VT\ge\left(x+y\right)^2+1-\dfrac{\left(x+y\right)^2}{4}=\dfrac{3\left(x+y\right)^2}{4}+1\)
Áp dụng Cô-si:
\(\dfrac{3\left(x+y\right)^2}{4}+1\ge2\sqrt{\dfrac{3\left(x+y\right)^2}{4}.1}=\sqrt{3}\left|x+y\right|\ge\sqrt{3}\left(x+y\right)\)
Do đó:
\(\left(x+y\right)^2+1-xy\ge\sqrt{3}\left(x+y\right),\forall x,y\in R\)

a: Ta có: \(\left(x+y\right)^2\)
\(=x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)
a\(\Leftrightarrow x^2+y^2+2\ge2x+2y\)
\(\Leftrightarrow\left(x^2-2x+1\right)+\left(y^2-2y+1\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-1\right)^2\ge0\)(luôn luôn đúng
=> BĐT đượcchứng minh
b/ \(\Leftrightarrow m^2+2m+1-4m\ge0\)
\(\Leftrightarrow m^2-2m+1\ge0\)
\(\Leftrightarrow\left(m-1\right)^2\ge0\)(luôn luôn đúng )
=> BĐT dược chứng minh