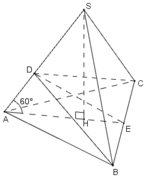
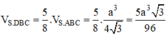Cho hình chóp đều S.ABC, SA=a. Gọi D, E là trung điểm của SA, SC.
1, Tính thể tích khối chóp SABC theo a, biết BD vuông góc AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
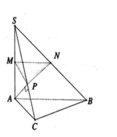
Xét tam giác SAC vuông tại A có AP là đường cao, ta có:
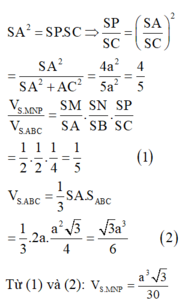

Gọi D là trung điểm của cạnh AB và O là tâm của tam giác ABC.
Ta có \(\begin{cases}AB\perp CD\\AB\perp SO\end{cases}\) nên \(AB\perp\left(SCD\right)\)
Do đó \(AB\perp SC\)
Mặt khác \(SC\perp AH\) suy ra \(SC\perp\left(ABH\right)\)
Ta có : \(CD=\frac{a\sqrt{3}}{2};OC=\frac{a\sqrt{3}}{2}\) nên \(SO=\sqrt{SC^2-OC^2}=\frac{a\sqrt{33}}{3}\)
Do đó : \(DH=\frac{SO.CD}{SC}=\frac{a\sqrt{11}}{4}\Rightarrow S_{\Delta ABH}=\frac{1}{2}AB.DH=\frac{\sqrt{11}a^2}{8}\)
Ta có : \(SH=SC-HC=SC-\sqrt{CD^2-DH^2}=\frac{7a}{4}\)
Do đó : \(V_{S.ABH}=\frac{1}{3}SH.S_{\Delta ABH}=\frac{7\sqrt{11}a^3}{96}\)
V(SABC) = SA.S(ABC)/3 = 2a.(a√3/2).a/6 = a^3√3/6
gọi khoảng cách từ A đến mp(SBC) là h, ta có:
V1 = V(SAMN) = V(ASMN) = S(SMN).h/3
V = V(SABC) = V(ASBC) = S(SBC).h/3
=> V1/V = S(SMN)/S(SBC) = 1/2.SM.SN.sin(MSN^)/1/2.SB.SC.sin(MSN^) = (SM/SB).(SN/SC)
SB = SC (do AB = AC) và SM = SN ( = SA^2/SB)
=> V1/V = (SM/SB)^2
SB^2 = SA^2 + AB^2 = 4a^2 + a^2 = 5a^2 => SB = a√5
SM = SA^2/SB = 4a^2/(a√5) = 4a/√5
=> V1/V = (16a^2/5)/(5a^2) = 16/25
=> (V - V1)/V = 9/25
=> V(A.BCNM) = (V - V1) = 9.V/25 = 9.(a^3√3/6)/25 = 3a^3√3/50

Phương pháp:
+) Thể tích của tứ diện vuông có độ dài các cạnh góc vuông là a, b, c là: V = 1 6 a b c
+) Sử dụng công thức tỉ số thể tích Simpson
Cách giải:
S.ABC là tứ diện vuông tại đỉnh S
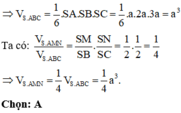

S H = S A 2 - A H 2 = a
Thể tích khối chóp S.ABC là:
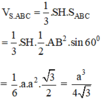
⇒ Thể tích khối chóp S.DBC là: