Question

[Linh]

Tìm giá trị của m để S=3-4m²/1-m⁴ đạt giá trị Lớn nhất

Answer 1

[Mr Lazy]

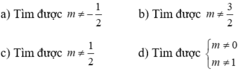
ĐK: \(x\ne1;\text{ }-1\)

\(S=\frac{3-4m^2}{1-m^4}\Leftrightarrow\left(1-m^4\right)S=3-4m^2\Leftrightarrow S.m^4-4m^2+3-S=0\)

Đặt \(m^2=x\text{ }\left(x\ge0\right)\)

Pt thành \(S.x^2-4x+3-S=0\text{ (*)}\)

\(+S=0\text{ thì }pt\text{ thành }0-4x+3-0=0\Leftrightarrow x=\frac{3}{4}\)

\(+\text{Xét }S\ne0;\text{ }\left(\text{*}\right)\text{ là một }pt\text{ bậc 2 ẩn }x;\text{ tham số }S;\text{ để tồn tại }x\text{ thì }\Delta'\ge0\)\(\text{Mà }\Delta'=2^2-S\left(3-S\right)=S^2-3S+4=\left(S-\frac{3}{2}\right)^2+\frac{7}{4}>0\text{ với mọi }S\ne0\)

Nên \(\left(\text{*}\right)\text{ có 2 nghiệm phân biệt }x_1;\text{ }x_2\text{ với mọi }S.\)

\(\text{Theo định lí Vi-et: }x_1+x_2=\frac{4}{S};\text{ }x_1.x_2=\frac{3-S}{S}\)

Để tồn tại m thì (*) phải có nghiệm \(x\ge0\). Xét 2 trường hợp:

+(*) có 2 nghiệm x₁; x₂ không âm

\(\text{Do }x_1;\text{ }x_2\ge0\text{ nên }x_1+x_2\ge0\text{ và }x_1.x_2\ge0\)

\(\Rightarrow\frac{4}{S}\ge0\) và \(\frac{3-S}{S}\ge0\)\(\Rightarrow0<\)\(S\le3\)

+(*) có 1 nghiệm âm và 1 nghiệm không âm.

\(\Rightarrow\frac{3-S}{S}\le0\Leftrightarrow S<0\text{ hoặc }S\ge3\)

Đến đây ta thấy (*) luôn có 1 nghiệm dương với mọi S thuộc R. Điều đó có nghĩa là, với số S lớn cỡ nào đi nữa luôn tìm được \(x>0\), hay nói cách khác, luôn tìm được m thỏa \(\frac{3-4m^2}{1-m^4}=S\). 

Vậy không tồn tại GTLN của S.

(Lưu ý: bấm máy tính ta cũng được kết quả như vậy.

Thử bấm tính S với m = 1,000000001, ta sẽ thấy S có giá trị rất lớn.

Nếu yêu cầu tìm GTNN thì bấm m = 0,99999999 thấy S có giá trị âm rất nhỏ.)

Tập giá trị của S là R, S không có GTLN; GTNN.