Tìm giá trị của x: \(\sqrt{2x-1}+5< 2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
7 tháng 7 2021
1.
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$A=|x+2|+|x+3|=|x+2|+|-x-3|\geq |x+2-x-3|=1$
Vậy GTNN của $A$ là $1$. Giá trị này đạt tại $(x+2)(-x-3)\geq 0$
$\Leftrightarrow (x+2)(x+3)\leq 0$
$\Leftrightarrow -3\leq x\leq -2$
AH
Akai Haruma
Giáo viên
7 tháng 7 2021
2. ĐKXĐ: $x\geq 1$
\(B=\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=\sqrt{(x-1)+2\sqrt{x-1}+1}+\sqrt{(x-1)-2\sqrt{x-1}+1}\)
\(=\sqrt{(\sqrt{x-1}+1)^2}+\sqrt{(\sqrt{x-1}-1)^2}=|\sqrt{x-1}+1|+|\sqrt{x-1}-1|\)
\(=|\sqrt{x-1}+1|+|1-\sqrt{x-1}|\geq |\sqrt{x-1}+1+1-\sqrt{x-1}|=2\)
Vậy gtnn của $B$ là $2$. Giá trị này đạt tại $(\sqrt{x-1}+1)(1-\sqrt{x-1})\geq 0$
$\Leftrightarrow 1-\sqrt{x-1}\geq 0$
$\Leftrightarrow 0\leq x\leq 2$
29 tháng 7 2021
a) Ta có: \(P=\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
AH
Akai Haruma
Giáo viên
20 tháng 9 2023
Lời giải:
a. Để bt có nghĩa thì $x^2-x+1\geq 0$
$\Leftrightarrow (x-\frac{1}{2})^2+\frac{3}{4}\geq 0(*)$
$\Leftrightarrow x\in\mathbb{R}$ (do $(*)$ luôn đúng với mọi số thực $x$)
b.
Để bt có nghĩa thì $x^2-5\geq 0$
$\Leftrightarrow (x-\sqrt{5})(x+\sqrt{5})\geq 0$
$\Leftrightarrow x\geq \sqrt{5}$ hoặc $x\leq -\sqrt{5}$
c.
Để bt có nghĩa thì: $-x^2+2x-1\geq 0$
$\Leftrightarrow -(x^2-2x+1)\geq 0$
$\Leftrightarrow x^2-2x+1\leq 0$
$\Leftrightarrow (x-1)^2\leq 0(*)$
Do $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$
Nên $(*)\Leftrightarrow (x-1)^2=0$
$\Leftrightarrow x=1$
d.
Để bt có nghĩa thì \(\left\{\begin{matrix} x-1\neq 0\\ \frac{-2}{x-1}\geq 0\end{matrix}\right.\Leftrightarrow x-1<0\Leftrightarrow x<1\)
16 tháng 8 2021
a: ĐKXĐ: \(x\ge\dfrac{1}{3}\)
b: ĐKXĐ: \(x< \dfrac{15}{2}\)
c: ĐKXĐ: \(x\le0\)
AT
10 tháng 7 2021
a) \(B=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\left(x\ge0,x\ne1\right)\)
\(=\left(\dfrac{2\sqrt{x}+x}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x+\sqrt{x}+1-\sqrt{x}-2}{x+\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}+x-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x-1}{x+\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{x+\sqrt{x}+1}{x-1}=\dfrac{1}{x-1}\)
13 tháng 8 2021
a,\(A=2\sqrt{x^2+x+\dfrac{1}{2}}=2\sqrt{x^2+x+\dfrac{1}{4}+\dfrac{1}{4}}=2\sqrt{\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{4}}\)
\(=\sqrt{4\left(x+\dfrac{1}{2}\right)^2+1}\ge1\) dấu"=" xảy ra<=>x=-1/2
\(B=\sqrt{2\left(x^2-2x+\dfrac{5}{2}\right)}=\sqrt{2\left[x^2-2x+1+\dfrac{3}{2}\right]}\)
\(=\sqrt{2\left(x-1\right)^2+3}\ge\sqrt{3}\) dấu"=" xảy ra<=>x=1
\(C=\dfrac{x-3}{\sqrt{x-1}-\sqrt{2}}\ge\dfrac{-2}{-\sqrt{2}}=\sqrt{2}\) dấu"=" xảy ra<=>x=1
\(D=x-2\sqrt{x+2}\ge-2\) dấu"=" xảy ra<=>x=-2
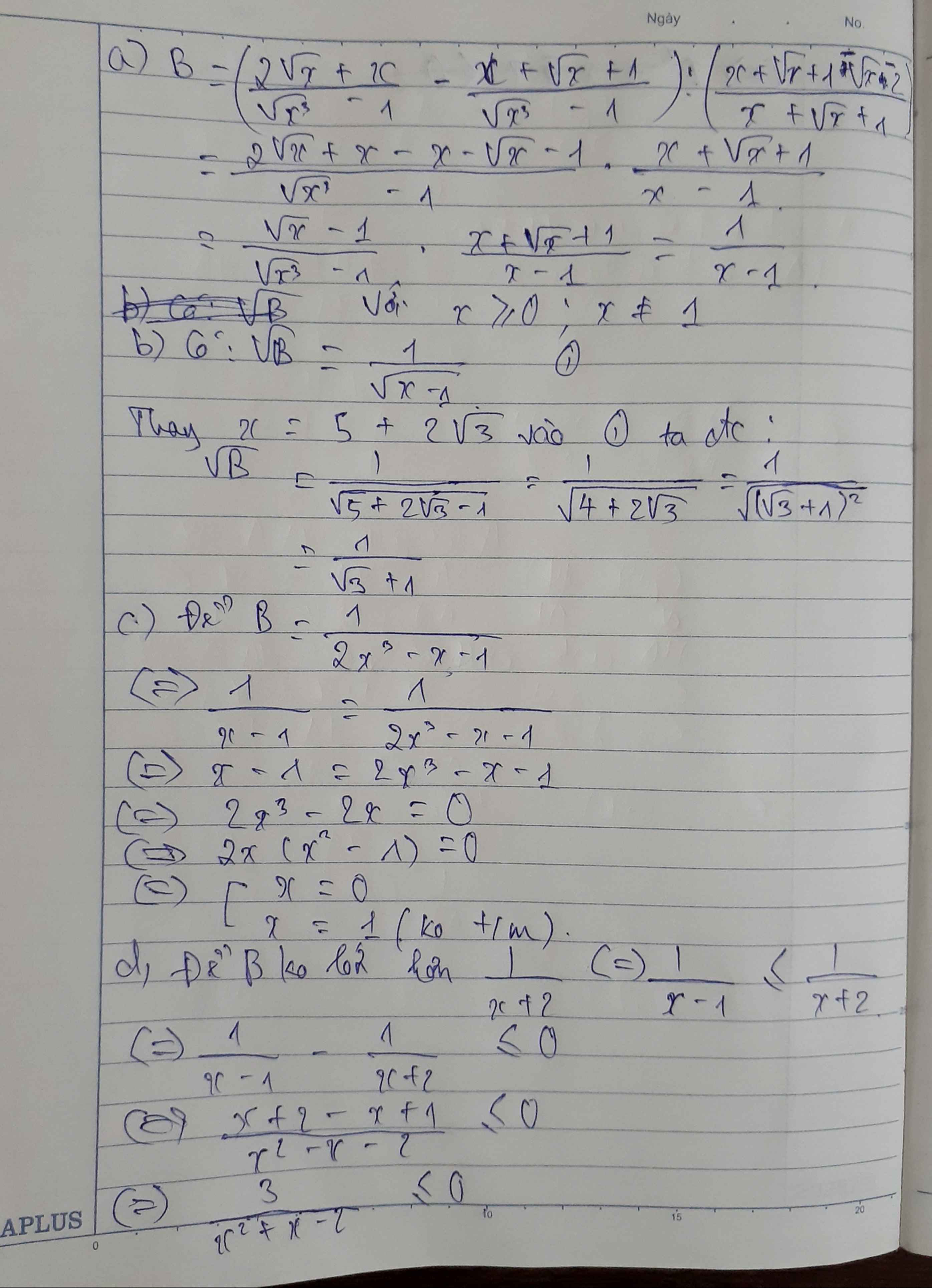
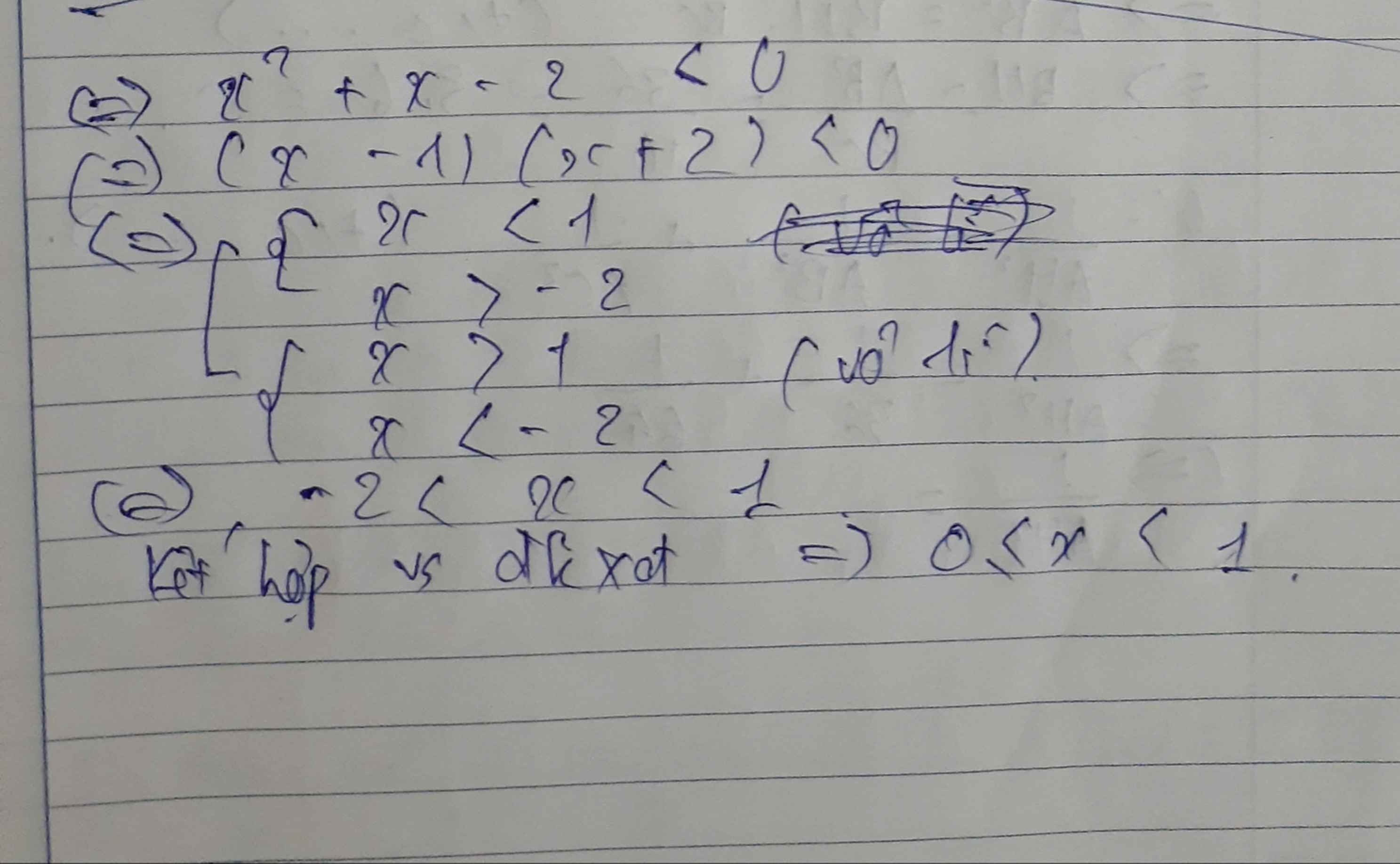
\(\sqrt{2x-1}+5< 2\)
\(\sqrt{2x-1}< -3\) ( sai vì \(\sqrt{2x-1}\ge0\forall x\)
Vậy pt vô nghiệm